1

I was playing around with some combinatorial expressions and tried to simplify the expression $\binom{k^2+k}{k^2-k}$. I got stuck at the point $\prod_{m=1}^{m=2k} \frac{k^2-k+m}{m}$ so I plugged the expression $\binom{k^2+k}{k^2-k}$ into Wolfram Alpha and got the following equivalent integral representations click to open integral representations 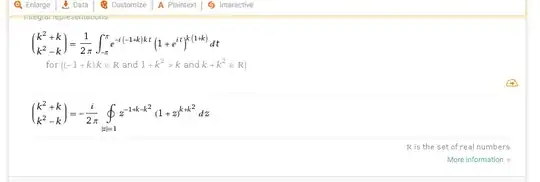I would like to know what resources I should use to learn about how this simplification occurs. Currently I am knowledgeable about single-variable Calculus, multi-variable Calculus, and differential equations, the latter two to a much lesser extent.

blue apples
  • 95

1 Answers1

2

The right-hand side is $\sum_{j=0}^{k(k+1)}\frac{1}{2\pi}\int_{-\pi}^{\pi}\binom{k(k+1)}{j}\exp i(j+k-k^2)tdt$. But any integer $l$ satisfies $$\frac{1}{2\pi}\int_{-\pi}^\pi\exp iltdt=\delta_{l0},$$so the only surviving term has $j=k^2-k$.

J.G.
  • 115,835
  • @kjetilbhalvorsen It looks like a complete expression for the right-hand side to me. What's missing? – J.G. Nov 27 '18 at 21:00
  • 1
    Writing a binomial as a complex integral is classical, and is a powerful method of investigation/proof. See for example https://math.stackexchange.com/q/1215985 – Jean Marie Nov 27 '18 at 22:22
  • I was more looking for resources that would help me understand where that expression comes from because as of right now, it's completely alien to me. As I said in my original post, I am knowledgeable about single-variable Calculus, multi-variable Calculus, and Differential Equations, though the latter two to a much lesser extent. What should I look at to be able to understand this myself? – blue apples Nov 28 '18 at 14:41