Just in case there's any way to simplify this integral or at least transform it to something which is easy to integrate numerically:
$$I(a,b,c)=\int_0^1 r J_0(ar)J_0(br)J_0(cr)dr$$
I'm interested in the case where $a,b$ are zeros of $J_0(x)$, $c>0$ is arbitrary real number.
There are a few papers dealing with similar integrals, but usually over an infinite domain, and in any case, nothing promising.
https://www.osapublishing.org/josaa/abstract.cfm?uri=josaa-7-7-1218
https://arxiv.org/abs/1006.4417
There's a related question for spherical Bessel functions here Integral over triple product of spherical Bessel functions, but I don't believe it's helpful.
From the sources above it's clear that there's no exact expression for the general case, however I would be interested in a way to speed up numerical integration and to deal with oscillations for large $a,b,c$.
I understand that we could use asymptotics for the large arguments, however we would have to separate the domain of integration somehow to accomodate for $r$ close to $0$. Not sure how to do that for the general case of $a,b,c$ so it could be made into an algorithm.
A related integral, which appeared in the same problem is:
$$Y(n,a,b)=\int_0^1 r K_0(\pi n r)J_0(ar)J_0(br)dr$$
Where $n$ is an integer, $a,b$ - zeros of $J_0(x)$. Maybe this one can be simplified?
Edit.
Some useful relations. From this paper we get an approximation:
$$J_0(x) \approx \frac{1}{6} \left(1+\cos x+2 \cos \frac{x}{2}+2 \cos \frac{\sqrt{3} x}{2} \right)$$
With the error terms approximated by $-2J_{12}(x)$. This approximation is quite good for $x \leq 5$ and may allow us to approximate the integral for small parameters much better than the Taylor series.
If we transform two of the Bessel functions that way, we will eventually get several integrals in the form:
$$\int_0^1 r \cos (s r) J_0(a r) dr=\frac{\partial }{\partial s} \int_0^1 \sin (s r) J_0(a r) dr$$
$$\int_0^1 r \sin (s r) J_0(a r) dr=-\frac{\partial }{\partial s} \int_0^1 \cos (s r) J_0(a r) dr$$
This doesn't look so bad.
And for the larger arguments we could use the asymptotic:
$$J_0(x) \asymp \sqrt{\frac{2}{\pi x}} \cos \left(x-\frac{\pi}{4} \right)$$
Using it for two functions will give us integrals in the form (similar to above):
$$\int_0^1 \cos (s r) J_0(a r) dr \\ \int_0^1 \sin (s r) J_0(a r) dr$$
It's quite useful that we have:
$$ \int_{0}^{\infty} J_{n}(bx) e^{-iax} dx=\begin{cases} \frac{-i e^{i \pi n /2} \left(\sqrt{a^{2}-b^{2}}-a \right)^{n}}{b^{n} \sqrt{a^{2}-b^{2}}}, & a>b \\ \frac{e^{-in \arcsin \left(\frac{a}{b}\right)}}{\sqrt{b^{2}-a^{2}}}, & a < b\end{cases}$$
We can express, for example:
$$\int_0^1 \cos (s r) J_0(a r) dr=\int_0^\infty \cos (s r) J_0(a r) dr-\int_1^\infty \cos (s r) J_0(a r) dr$$
Where the last integral can again be approximated through the Bessel function asymptotic and expressed through Fresnel integrals.
This relation may be useful as well, though the singular integral is not the best choice for numerical evaluation:
$$J_0(x)=\frac{2}{\pi} \int_0^1 \frac{\cos x u}{\sqrt{1-u^2}}du$$
Though I suppose we could use Chebyshev-Gauss quadrature here to avoid the singularity. From a quick numerical experiment we should pick $n \approx x$, then we get very accurate expression:
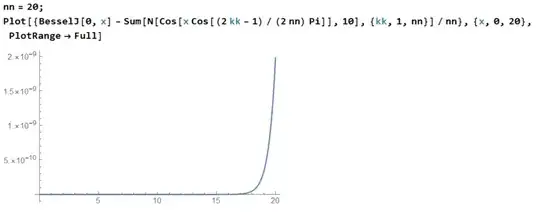
$$J_0(x) \approx \frac{1}{n} \sum_{k=1}^n \cos \left(x \cos \left( \frac{2k-1}{2n} \pi \right) \right)$$
This may be even better than any approximation above, as it works in a greater domain provided we pick $n$ large enough.
Here's an example for $n=20$, which shows that the approximation is very good.
It will take some work to correctly implement all of these approximations, in the meantime I would be greatful for some additional advice.