Regular polygons with common side

Question

Given a segment $AB$ in the plane, draw all possible regular polygons having $AB$ as a side.

Is it true that if a line contains infinitely many vertices of those polygons, then that line contains either $A$, or $B$, or the midpoint of $AB$?

Answer 1

The coordinates of the $k$th vertex of a regular $n$-gon $(O,R)$ $\,$ are $\,$ $\Big(R\cos{2k\pi\over n},R\sin{2k\pi \over n}\Big)$. (O(0,0))

Without loss of generality let the $n$-gon's side be $α=2$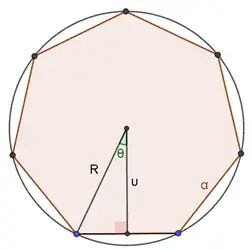

${υ\over R}=\cos{\frac{\pi}{n}} \quad (1)\\ υ^2 +1^2=R^2 \quad (2)$

$(1),(2)\Longrightarrow υ=\cot{\pi\over n} \quad $and $\quad R={1\over \sin{\pi\over n}}$

Therefore, the coordinates of the $k$th vertex of a regular $n$-gon $(O,R)$ $\,$ are $\,$$\Big({\cos{2k\pi\over n}\over \sin{\pi\over n}},{\sin{2k\pi \over n}\over \sin{\pi\over n}}\Big)$

• So that $,$ $N_0N_{n-1}\parallel x’x $ we rotate the polygon by $\frac{\pi}{n}-\frac{\pi}{2}$ rad around $O$ (rotation)

  our new $k$th vertex has coordinates $\Big(\cos{2k\pi\over n}+\cot{\pi\over n}\sin{2k\pi\over n},\sin{2k\pi\over n}-\cot{\pi\over n}\cos{2k\pi\over n} \Big)$

$\\$

• So that $,$ $N_0N_{n-1}\in{x’x}$, we have to add $υ=\cot{\pi\over n}$ to the y coordinates

Finally ,we end up with the coordinates: $K_{n}^{k}\Big(\cos{2k\pi\over n}+\cot{\pi\over n}\sin{2k\pi\over n},\sin{2k\pi\over n}-\cot{\pi\over n}\cos{2k\pi\over n} +\cot{\pi \over n} \Big)$

which are equal to $K_{n}^{k}\Big(2\frac{\cos{(\frac{(k+1)\pi}{n})}\sin{k\pi\over n}}{\sin{\pi\over n}}+1, 2\frac{\sin{(\frac{(k+1)\pi}{n})}\sin{k\pi\over n}}{\sin{\pi\over n}} \Big)$

and also equal to
$K_{n}^{k}\Big(2\overset{k}{\underset{i=1}{\sum}}(\cos{2i\pi\over n})+1,2 \overset{k}{\underset{i=1}{\sum}}(\sin{2i\pi\over n}) \Big)$ $\quad$ see identity

and also equal to $K_{n}^{k}\Big( \frac{\cos{(\frac{(2k+1)\pi}{n})}}{\sin{\pi\over n}},2\frac{\sin{(\frac{(k+1)\pi}{n})}\sin{k\pi\over n}}{\sin{\pi\over n}} \Big)$

Which vertices does the line passing through $K_{n}^{0}$ (Point B in the original question) contain?

The line which contains $K_{n}^{0}$ is $\quad$ $(l):y=a(x-1)$

$K_{n}^{k}\in (l):y=a(x-1)\iff 2\frac{\sin{(\frac{(k+1)\pi}{n})}\sin{k\pi\over n}}{\sin{\pi\over n}}=a\Big( 2\frac{\cos{(\frac{(k+1)\pi}{n})}\sin{k\pi\over n}}{\sin{\pi\over n}}+1-1 \Big)\iff \frac{\sin{(\frac{(k+1)\pi}{n})}\sin{k\pi\over n}}{\sin{\pi\over n}}=a\frac{\cos{(\frac{(k+1)\pi}{n})}\sin{k\pi\over n}}{\sin{\pi\over n}} \iff \sin{(\frac{(k+1)\pi}{n})}\sin{k\pi\over n}=a\cos{(\frac{(k+1)\pi}{n})}\sin{k\pi\over n}\iff \Big( \sin{k\pi\over n}=0\Big) \lor \Big(\tan{{{k+1}\over n}\pi}=a\Big) \quad (3) $

$\tan{{{k+1}\over n}\pi}=a\overset{a=\tan u}{\iff} {{k+1}\over n}\pi = u +z\pi,\quad z\in\mathbb{Z} \overset{u={m\over n}\pi}{\iff} m=k+1-zn, \quad \gcd{(m,n)}=1 $

Using this we find for example that the line described by: $y=\frac{\sqrt{3}}{3}(x-1)$ contains all vertices satisfying $n=6k+6$

$\\$ We can restate the problem equivalently ,algebraically :

$\exists ^{\infty} (n,k): 2 \overset{k}{\underset{i=1}{\sum}}(\sin{2i\pi\over n})=a\Big( 2\overset{k}{\underset{i=1}{\sum}}(\cos{2i\pi\over n})+1 \Big) +b ,\quad a,b\in{\mathbb{R}}\\ \Longrightarrow (b=a)\lor (b=-a)\lor (b=0) $

or

$\exists ^{\infty} (n,k): 2\frac{\sin{(\frac{(k+1)\pi}{n})}{{\sin{k\pi \over n}}}}{\sin{\pi\over n}}=a\Big(\frac{\cos{(\frac{(2k+1)\pi}{n})}}{\sin{\pi\over n}} \Big)+b, ,a,b\in{\mathbb{R}} \Longrightarrow (b=a)\lor (b=-a)\lor (b=0) $

Similar problems, arguably simpler, have been solved [5],[6]

Answer 2

If we look at the polygons with $4n$ sides ($n\ge 2$)

We come close to finding a line where all polygons have a vertex on that line, and the line goes through neither A, B nor the midpoint of AB. It's not exact, but in mathematics appearances can be deceiving.

Answer 3

Partial answer, too long for a comment:

This is really just an attempt to establish what we're trying to solve in terms of complex numbers, where colinearity may be easier to describe, etc. $ \newcommand{\i}{\mathbf{i}}$ If we rotate 90 degrees, and work in the complex plane, placing $A$ at $+\i$ and $B$ at $-\i$, and only look in the right half-plane (because...symmetry!), then the polygon centers are all on the real line. The center of polygon $n$ is at $$ c_n = \sec \frac{\pi}{n} + 0 \i $$ and the $k$th point of that polygon is at $$ u_{n,k} = c_n + (\sec \frac{k\pi}{n} + \i \csc \frac{k\pi}{n}). $$