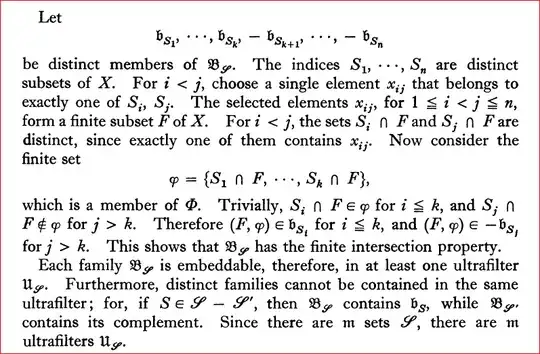10

I'm stuck with the next exercise from the book Rings of Continuous Functions by Gillman.

If $X$ is infinite, there exist $2^{2^{|X|}}$ ultrafilters on $X$ all of whose members are of cardinal $X$.

The exercise have a hint based on the next proof (here $\beta X$ is the Stone–Čech compactification)

enter image description here

enter image description here

In the proof, the author constructs $2^{2^{X}}$ distinct ultrafilters on $X$. The hint of the exercise says

In the proof of Theorem 9.2, observe that every finite intersection of members of $\mathfrak{B}_{\mathscr{S}}$ is of cardinal $|X|$. Adjoin to each family $\mathfrak{B}_{\mathscr{S}}$ all subsets of $\mathscr{F}\times\Phi$ with complement of power less than $|X|$.

I'm stuck in the two parts of the hint. I don't know how can I prove that every finite intersection of elements of $\mathfrak{B}_{\mathscr{S}}$ is of cardinal $|X|$. I only know that because $\mathfrak{b}_{S_{i}}\subseteq \mathscr{F}\times \Phi$ and $-\mathfrak{b}_{S_{j}}\subseteq \mathscr{F}\times \Phi$ then $|\mathfrak{b}_{S_{i}}|\leq|X|$ and then $|-\mathfrak{b}_{S_{j}}|\leq |X|$. Therefore $$|\mathfrak{b}_{S_1}\cap\mathfrak{b}_{S_2}\cap\dots\cap,\mathfrak{b}_{S_k}\cap-\mathfrak{b}_{S_{k+1}}\cap\dots\cap-\mathfrak{b}_{S_n}|\leq|\mathfrak{b}_{S_1}|\leq|X|$$But, how can I conclude the another inequality?, i.e., $$|\mathfrak{b}_{S_1}\cap\mathfrak{b}_{S_2}\cap\dots\cap,\mathfrak{b}_{S_k}\cap-\mathfrak{b}_{S_{k+1}}\cap\dots\cap-\mathfrak{b}_{S_n}|\geq|X|$$And, how can it helps to consider the subsets of $\mathscr{F}\times\Phi$ with complement of power less than $|X|$? I think the approach I've taken is so hard or there are something that I can't see because the proof looks so hard for me.

Community
  • 1
Carlos Jiménez
  • 3,895

1 Answers1

3

To show that all finite intersections of sets in $\mathfrak{B}_{\mathscr{S}}$ have cardinality $|X|$ it suffices just to construct $|X|$-many elements in the intersection. (This is because, as you have noticed, there cannot be more than $|X|$-many elements in the intersection.)

In the proof given, we have one particular element of this intersection: $$( F = \{ x_{ij} : i \neq j \} , \varphi = \{ F \cap S_1 , \ldots , F \cap S_k \} ).$$ Suppose that $( F , \psi ) \in \mathscr{F} \times \Phi$ is such that $\phi \supseteq \varphi$ is finite. Given any $i \leq k$ note that we clearly have that $S_i \cap F \in \psi$, and so $( F , \psi ) \in \mathfrak{B}_{S_i}$. Given $k < j \leq n$ note that $( F , \psi ) \in - \mathfrak{b}_{S_j}$ as long as $S_j \cap F \notin \psi$. Therefore as long as $\psi \supseteq \phi$ is chosen so that $F \cap S_{k+1} , \ldots , F \cap S_{n} \notin \psi$, then $( F , \psi )$ will belong to the intersection. There are clearly $|X|$-many ways to choose appropriate $\psi$.

Let $\mathfrak{B} = \{ \mathscr{A} \subseteq \mathscr{F} \times \Phi : | ( \mathscr{F} \times \Phi ) \setminus \mathscr{A} | < |X| \}$ denote the family of all subsets of $\mathscr{F} \times \Phi$ with complement of power $< |X|$. Note that not only does $\mathfrak{B}$ have the finite intersection property, it is actually closed under finite intersections.

With this observation and the work above it becomes relatively easy to show that given $\mathscr{S} \subseteq \mathcal{P} ( X )$ the family $\mathfrak{B}_{\mathscr{S}} \cup \mathfrak{B}$ has the finite intersection property. To see this, suppose that $\mathfrak{b}_{S_1} , \ldots , \mathfrak{b}_{S_k} , - \mathfrak{b}_{S_{k+1}} , \ldots , - \mathfrak{b}_{S_n} , \mathscr{A}_1 , \ldots , \mathscr{A}_m$ are given. Then

  • by the work above the set $\mathfrak{b} = \mathfrak{b}_{S_1} \cap \cdots \cap \mathfrak{b}_{S_k} \cap - \mathfrak{b}_{S_{k+1}} \cap \cdots \cap - \mathfrak{b}_{S_n}$ has power $|X|$, and
  • by the observation above the complement of $\mathscr{A} = \mathscr{A}_1 \cap \cdots \cap \mathscr{A}_m$ has power $< |X|$.

Thus $\mathfrak{b} \cap \mathscr{A} \neq \emptyset$.

Therefore this family can be extended to an ultrafilter $\mathfrak{U}_{\mathscr{S}}$, and since $\mathfrak{B} \subseteq \mathfrak{U}_{\mathscr{S}}$, we know that $\mathfrak{U}_{\mathscr{S}}$ cannot include any sets of power $< |X|$.

stochastic randomness
  • 537