20

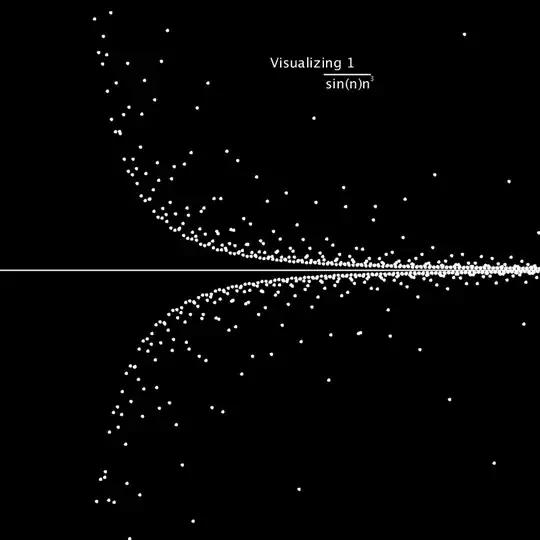
Does the sequence $$a(n) = \frac{1}{n^3\sin(n)}$$ converge ?

I tried all possible standard calculus approaches but to no avail ...

edit:

I tried using the root theorem and the limit of the $\frac{a_{n+1}}{a_{n}}$ which kinda got me nowhere ... Then I followed it with trying to prove that $n^3\cdot \sin(n)$ has no lower bound $K > 0$ by checking the behavior of the function $|n^3\cdot \sin(n)|$ and concluding that at some point the integer value of $n$ will bring me the value of function, which will be between $0$ and $K$, but I failed to give a rigorous proof of that conclusion

Rustyn
  • 8,407
Makina
  • 1,454
  • 2
    What standard calculus approaches did you try, and can you show your work from one such approach? – amWhy Nov 14 '18 at 19:19
  • @amWhy I tried using the root theorem, which gave me 1 in the limit, and the limit of the $\frac{a_{n+1}}{a_{n}}$ which kinda got me nowhere either ... Then I followed it with trying to prove that n3∗sin(n) has no lower bound K >0 by checking the behavior of the function |n3∗sin(n)| and concluding that at some point the integer value of n will bring me the value of function, which will be between 0 and K, but I failed to give a rigorous proof of that conclusion. – Makina Nov 14 '18 at 19:44
  • 1
    I think that since Makina, has included what they tried in the comments, the close votes should be retracted... – Rustyn Nov 14 '18 at 20:00
  • 5
    This is related to Flint Hills series. The convergence of such sequence depends on the irrationality measure of $\pi$. – Sungjin Kim Nov 14 '18 at 20:08
  • A related question on MO: https://mathoverflow.net/q/24579 –  Nov 14 '18 at 20:11
  • @Makina: Please include your comment in your question itself, to provide context. Thanks! – user21820 Nov 15 '18 at 14:19
  • @user21820 fair enough, added – Makina Nov 15 '18 at 16:54
  • Since you mentioned the root test and ratio test, I think what you really asking is the convergence of the series $\sum_{n=1}^\infty\frac{1}{n^3\sin(n)}$, not the sequence $a_n$? They are of course related though. –  Nov 16 '18 at 01:10

2 Answers2

23

The answer to this question depends on the irrationality measure $\mu(\pi)$ of $\pi$, in a way which means it is unsolved. (The current state of the art is that $2 \leq \mu(\pi) \leq C$, where $C \approx 7.6$.)

Suppose that $\mu(\pi)>4$. Then there exist infinitely many pairs of integers $(p,q)$ such that

$$\left|\pi - \frac{p}{q}\right|<\frac{1}{q^4}$$

For such a $p$, $|\sin p|=|\sin(p-q\pi)|<|q\pi - p|<\frac{1}{q^3}$ and so $$ \left|\frac{1}{p^3\sin p}\right|>\frac{q^3}{p^3}>\frac{1}{27} $$ (as $\frac{p}{q}$ closely approximates $\pi$, so in particular it will be greater than $3$). Since the sequence can only converge to zero, this is enough to show that it diverges.

On the other hand, suppose the sequence diverges. Then there is some constant $C$ and subsequence $(p_n)$ such that $$\left|\frac{1}{(p_n)^3\sin p_n}\right|>C$$ for all $n$. Choose $q_n$ so that $|p_n-\pi q_n|<\frac{\pi}{2}$. Then we have $$ |\pi q_n-p_n|<\frac{\pi}{2}|\sin(p_n-\pi q_n)|=\frac{\pi}{2}|\sin p_n|<\frac{1}{C (p_n)^3} $$ and so $$ \left|\pi-\frac{p_n}{q_n}\right|<\frac{1}{C(p_n)^3q_n}<\frac{1}{27C(q_n)^4} $$

for infinitely many $p_n,q_n$. This is enough to imply that $\mu(\pi)>4$.

So, in summary, finding whether the sequence converges essentially boils down to comparing $\mu(\pi)$ to $4$: a wildly unsolved problem.

Micah
  • 38,108
  • 15
  • 85
  • 133
  • Many thanks for this answer, I think it's the most complete yet. Somehow I knew that this question wasn't straightforward as one might expect... – Rustyn Nov 14 '18 at 20:53
  • 2
    (+1) for a nice answer that actually addresses how hard this is. For interested readers, there is this note that bounds the irrationality measure of $\pi$ in a fairly elementary way, although it's not the best known result anymore. –  Nov 14 '18 at 20:53
  • Does the exponent of $3$ matter? For other powers the sequence still has "poles" at multiples of $\pi$. –  Nov 14 '18 at 20:53
  • @M.Nestor A sufficiently large exponent there would force convergence. –  Nov 14 '18 at 20:54
  • 1
    @M.Nestor: If the exponent is larger than $\mu(\pi)-1$, the series converges. (So $\frac{1}{n^7 \sin n}$ is definitely convergent, but we're not sure about $\frac{1}{n^6 \sin n}$ yet.) – Micah Nov 14 '18 at 20:56
  • @Micah You meant "sequence", right? – Sungjin Kim Nov 15 '18 at 02:19
  • @i707107: In my comment that I can't edit? Yes. – Micah Nov 15 '18 at 02:23
9

Thought I would include a visualization for interested parties: Sequence

Rustyn
  • 8,407