On the power tower $\exp(x-\exp(x-\cdots))$

Question

The intention is to find the maximum of the power tower $\exp(x-\exp(x-\cdots))$. From here, we see that it is around $0.965$ or possibly even higher. The approximate value of its integral is also given for interest.

Since $\exp(x-\exp(x-\cdots))$ has this shape in the link for every two iterations, $$\exp(x-\exp(x-\cdots))=k\implies \exp(x-\exp(x-k))=k$$ not $\exp(x-k)=k$.

But we face a problem, how do we write $k$ purely in terms of $x$?

Answer 1

(0) $\qquad$ Let basically $f_0(x)=\exp(x)$ and then iterate $f_{k+1}(x)=\exp(x-f_k(x))$ a couple of times and assume $f(x)= \lim_{n\to \infty} f_n(x)$

---

(I) $\qquad$ First we assume all that in terms of a formal powerseries. Then this converges to something like $$ f_\infty(x) \approx +0.567143290410 \\ +0.361896256635 x^{1} \\ +0.0736778051764 x^{2} \\ -0.00134285965499 x^{3} \\ -0.00163606514791 x^{4} \\ +0.000232149655570 x^{5} \\ +0.0000474223203353 x^{6} \\ -0.0000189444233824 x^{7} \\ -0.0000000208785458195 x^{8} \\ +0.00000117699067908 x^{9} \\ -0.000000179633602646 x^{10} \\ -0.0000000510936764494 x^{11} \\ +0.0000000206028966316 x^{12} \\ +0.000000000306827812731 x^{13} \\ -0.00000000154503877033 x^{14} \\ + O(x^{15}) $$ using Pari/GP. Setting $x=1$ it approximates nicely the value $f(1)=1$. Moreover, for $x=0$ it gives immediately the value $\omega=0.5671432...=W(1)$

---

(II) $\qquad$ If we say $t:=f_\infty(x) $ and $t=\exp(x-t)$ then we can derive $t \exp(t) = \exp(x)$ and thus $ t=W(\exp(x)) = f_\infty(x) $ and this is $1$ for $x=1$ and $\omega$ for $x=0$ as before.

---

(III) $\qquad$ If we use the basic definition (but not as powerseries but as evaluated values) and take the mean $g_k = (f_k(x) + f_{k+1}(x))/2$ for some (high) iteration $k$ then $err_k(x)= g_k(x) -f_\infty(x) $ shows a small difference-curve increasing with $x \to 1$ but accordingly and in concurrence decreasing with $k \to \infty$ , so it seems also by this limiting-process that the definition of the limit using the Lambert-W-definition makes sense.

---

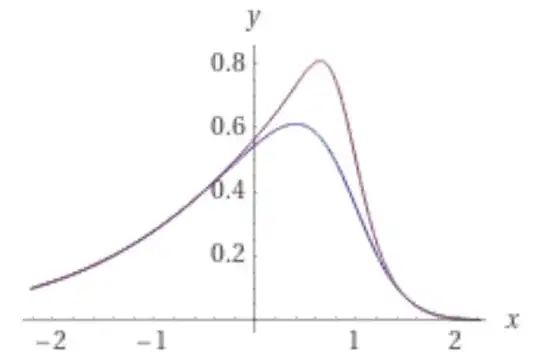
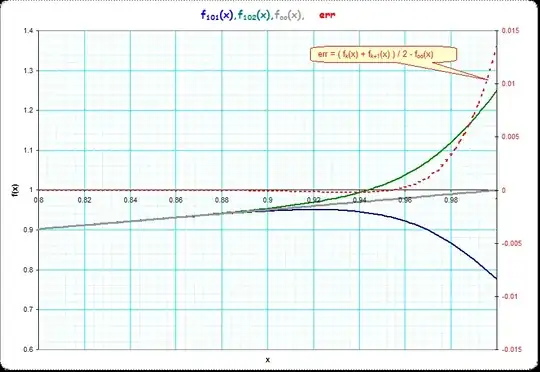
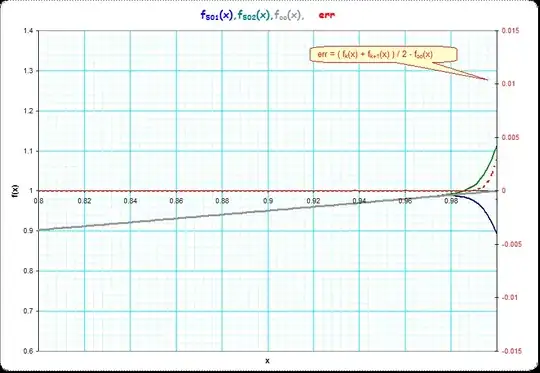
For (III) see the following pictures. The first picture shows $f_{101}(x),f_{102}(x),f_\infty(x),err_{101}(x)$ It makes visually that it makes sense to look at the mean of the alternating values $f_{101}(x)$ and $f_{102}$, and also, that the difference of the mean and the $f_\infty(x)$ is small but increasing somewhat when $x \to 1$ (the scale for the err-curve is at the rhs of the picture).

The second picture shows $f_{501}(x),f_{502}(x),f_\infty(x),err_{501}(x)$ and we see, that the two curves approximate the $f_\infty(x)$ curve much more which is displayed in the smaller $err_{501}(x)$

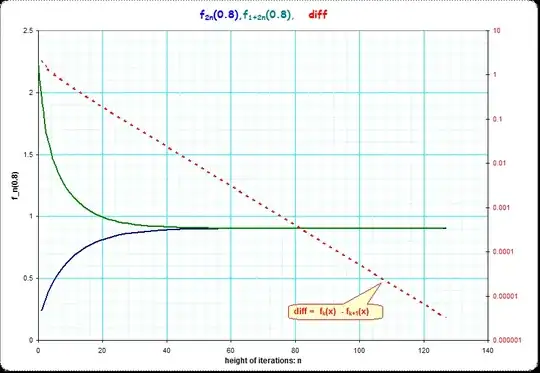
The third picture shows the rate of convergence improving by iterations. I use the value $x_0=0.8$ and document $t_n(x_0)=f_{2n}(x_0)$ and $u_n(x_0)=f_{2n+1}(x_0)$ for $1$ to $128$ iterations. We see that $t_n()$ and $u_n()$ converge well and the difference decreases by about one significant decimal digits by ca 12 iterations.

Answer 2

We have $\exp(x-\exp(x-k))=k$

Taking logarithm on both side we get :

$$xe^k-e^x=e^k\ln(k)$$

Your equality is of the form $(a,b,c\ne0)$: $$ae^x+bx+c=0$$ Where $a=-1$ , $b=e^k$ and $c=-e^k\ln(k)$

Let us find the general solution .

First it's equivalent to : $$\frac{a}{b}e^x+x+\frac{c}{b}=0$$ Or $$\frac{a}{b}e^x=-\left(x+\frac{c}{b}\right)$$ Or: $$\frac{b}{a}e^{-x}\left(-\left(x+\frac{c}{b}\right)\right)=1$$ Or: $$e^{-x-\frac{c}{b}}\left(-\left(x+\frac{c}{b}\right)\right)=\frac{a}{b}e^{-\frac{c}{b}}$$

Put $u=-x-\frac{c}{b}$ and $v=\frac{a}{b}e^{-\frac{c}{b}}$ wich gets :

$$ue^u=v$$

Then use the definition of the lambert function to have :$$x=f(k)$$

Next to get :

$$g(x)=k$$

You can use as primary tool the Lagrange Inversion Theorem

Answer 3

Series expansion for $k$

Via Lagrange reversion: $$k=e^{x-e^{x-k}} =\sum_{n=1}^\infty\frac{e^{nx}}{n!}\left.\frac{d^{n-1}}{dw^{n-1}}e^{-e^ke^{-w}}\right|_0$$

A table of derivatives implies Stirling S2:

$$\left.\frac{d^{n-1}}{dw^{n-1}}e^{pe^{-w}}\right|_0=(-1)^{n+1}e^p\sum_{m=0}^{n-1}s_{n-1}^{(m)}p^m$$

We notice this sum is formula $(14)$’s Bell polynomials. Therefore:

$$\bbox[5px, border:1px dashed blue]{k=\sum_{n=1}^\infty\frac{(-1)^{n+1}\operatorname B_{n-1}(-ne^x)}{e^{(e^x-x)n}n!}}$$

First 10 partial sums in purple and 3rd iteration of $\exp(x-\exp(\dots))$ in blue:

Integration

Integrating the function may require an expansion or two and the maximum, when graphing $k=e^{x-e^{x-k}}$, is $(1,1)$. The incomplete gamma function gives:

$$\int e^{sx}e^{-n e^x}dx=-\frac{\Gamma(s,ne^x)}{n^s}$$

so we use the 2,3 argument gamma regularized function:

$$\bbox[5px, border:1px dashed blue]{\int k(x) dx=C-\sum_{n=1}^\infty\sum_{m=n}^{2n-1}\frac{s_{n-1}^{(m-n)}(-1)^mQ(m,ne^x)}{n^{n+1}}\\\int_0^1 k(x)dx= \sum_{n=1}^\infty\sum_{m=n}^{2n-1}\frac{s_{n-1}^{(m-n)}(-1)^m Q(m,en,n)}{n^{n+1}}\approx 0.763}$$

The series converges more slowly near $x=1$, so here is a evaluator for the integral on $[0,1]$. Also, the plot when $C=0$ is:

Area under graph

Since $\int_{\Bbb R} e^{sx-ne^x}dx=\frac{\Gamma(s)}{n^s}$:

$$\int_{-\infty}^\infty k(x)dx=\sum_{n=1}^\infty\sum_{m=0}^{n-1}\frac{(-1)^{m+n-1}s_{n-1}^{(m)}n^m}{n!}\int_{-\infty}^\infty e^{(m+n)x}e^{-ne^x}dx=\sum_{n=1}^\infty\sum_{m=0}^{n-1}\frac{(m+n-1)!(-1)^{m+n-1}s_{n-1}^{(m)}}{n^n n!}$$

and OEIS result $\sum\limits_{m=0}^{n-1}(-1)^{m+n-1} (m+n-1)! s_{n-1}^{(m)}=\frac{n^{n-2}}{n!}$ gives a numerically plausible result:

$$\bbox[5px, border:1px dashed blue]{\int_{\Bbb R}\exp(x-\exp(x-\dots))dx=\frac{\pi^2}6}$$

Answer 4

You've noted $k=e^{x-k}$ so $ke^k=e^x$. In terms of the Lambert $W$ function, $k=W(e^x)$. The main question is which branch choice we take as our definition of the tower.