What does multiplying the integrand by $dx$ mean in an indefinite integral?

Question

I have two questions:

I just learned about U-Substitution in class, and while I'm able to apply it, I'm a bit confused on some of the theory behind it.

The thing that most confuses me is that if we take the indefinite integral of f '(x) with respect to "x", that means the term inside the integral is actually the multiplication of f '(x) and dx. I always thought that dx term was just there to show that the derivative was taken w.r.t. "x", I didn't know it was being multiplied by f '(x). Why is this the case?

I'm also just very confused on the integral in general. It seems to me that the integral of something can mean many different things (antiderivative, area under a curve). How are definite and indefinite integrals related and where do they come from?

edit: Please look to my comments on KM101's answer to better understand what I'm asking.

Answer 1

The indefinite integral of a function $f$ is any function $g$ such that $g'=f$. The definite integral of a real-valued function $f$ over the interval $[a,b]$ can be interpreted as the area under the curve which is the graph of $f$ over $[a,b]$.

You are right, the d$x$ in the integration stands for w.r.t. $x$. When doing $u$-substitution we think of $\frac{\text{d}u}{\text{d}x}$ as multiplying exclusively with d$x$ to obtain a new integration in terms of just $\text{d}u$ so that you can integrate with respect to $u$ now and remain with the same solution. The function $f$ and d$x$ are not meant to be multiplied in $\int f(x)\ \text{d}x$.

What really is going on here is that if $f$ and $g$ are two nice functions and we let $u=g$, then $$\int f(g(x))\ \text{d}x=\int f(u)u'\ \text{d}u$$

Answer 2

$dx$ indicates precisely what you said. It’s not really multiplication though.

In substitution, you would need to substitute $u$ and $\frac{du}{dx}$. Imagine you have the following integral. (Very simple example.)

$$\int (2x)^2 dx$$

$$\color{blue}{u = 2x} \implies \color{purple}{\frac{du}{dx} = 2}$$

$$\int \frac{1}{2}\cdot (2x)^2 \color{purple}{2}dx = \frac{1}{2}\int (2x)^2 2dx$$

$$\implies \color{blue}{du = 2dx}$$

$$\frac{1}{2} \int \color{blue}{u}^2 \color{blue}{du}$$

Which is easily solved.

The point is that $dx$ and $du$ show what variable you are integrating with respect to. When you change the variable, you need to integrate it with respect to that variable, so you carry out a process similar to the one above.

A definite integral is one that is restricted to the region between two $x$-coordinates. For instance:

$$\int 2x dx = x^2+C$$

$$\int_{1}^{4} 2x dx = 4^2+C-\big(1^2+C\big) = 16+C-1-C = 15$$

There, the integral was found in the region between $x = 1$ and $x = 4$. And yes, integrals are often related to the area under the curve, or in a more practical manner, “accumulation.”

Say you have an original function of $f(x)$. The derivative of the function, or $f’x$, shows the “instantaneous” rate of change. Integrating $f’x$ gives the accumulation, or area of the graph, which is the original function: $f(x)$. (Hence, integrals are often referred to as antiderivatives.)

You may want to check out Riemann sums and integrals to get a better idea.

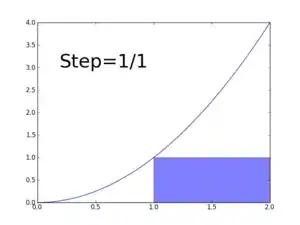
The basic idea is to divide the area under a curve into rectangles of a certain width, usually, but not always, the same width. The more you shrink down the width of the rectangles and increase the number of rectangles, the more you approach the true area.

For instance, say you choose the rectangles to be of equal width: $\Delta x$. If you choose the height of a rectangle to be the height at the point $f(x)$ (left-hand points), then each rectangle will have the area $\Delta x\cdot (f(x_i))$.

Thus, the area is the sum of all $n$ such rectangles.

$$A \approx \sum_{i = 1}^{n} \Delta x\cdot (f(x_i))$$

As $n$ keeps increasing, the number of rectangles will increase and the rectangles themselves will become thinner and thinner. ($n$ becomes infinitely large and $\Delta x$ becomes infinitely thin.)

$$A = \lim_{n \to \infty} \sum_{i = 1}^{n} \Delta x\cdot (f(x_i))$$

To observe this, you can try with a function. Say $f(x) = x^2$ and you would want to calculate the area between $x = 0$ and $x = 2$. Keep increasing $n$ and see what happens. (I’ll show left-hand side values. Right-hand side will also converge to the same value.)

$$n = 1 \implies A = 0$$

$$n = 2 \implies A = 1$$

$$n = 4 \implies A = 1.75$$

$$n = 8 \implies A = 2.1875$$

Keep continuing. For example:

$$n = 1024 \implies A \approx 2.66276$$

The more $n$ increases, the closer the value gets to $2.\overline{6}$. Checking the definite integral, that is exactly what you obtain: $\frac{8}{3}$. The animation below can make it clearer.

Answer 3

I think this question is the heart of your confusion. Once you understand the answer the formalities of substitution will no longer bother you.

It seems to me that the integral of something can mean many different things (antiderivative, area under a curve). How are definite and indefinite integrals related and where do they come from?

Well the answer to that question is a collection of results gathered under the name "the fundamental theorem of calculus." Needless to say, I won't provide a full discussion . There is lots about it on this site and in your text.

Here's a short version. If you think of the definite integral as the area under a curve over an interval, then you can find it as accurately as you wish without knowing any calculus. You divide the interval into many small intervals and build a rectangle over each that's approximately as high as the function, then add up the areas of the rectangles. Since the bases of the rectangles are small the height won't vary much over each. If you make the subdivisions of the interval smaller and smaller the errors in the rectangles will be smaller and in the limit you'll have the area you want.

If that sounds tedious, it is. Fortunately, there's a miracle discovered by Newton and Leibniz. They realized that there is a connection between differentiation (finding slopes) and integration (finding areas the hard way, as above). If you are lucky enough to guess an antiderivative for the function you want the area under, then that area is the difference between the values of the antiderivative at the end points of the interval.

In most elementary calculus courses you first learn the rules for differentiation, and then strategies for guessing antiderivatives. Your instructors are pretty careful and only ask you to do that when there really are antiderivatives with nice formulas.

This answer may be helpful: Why can't the second fundamental theorem of calculus be proved in just two lines?

Finally, a few words on $u$-substitution. In the notation for the definite integral $$ \int_a^b f(x)dx $$ you should think of $f(x)$ as the height of a rectangle with infinitesimal base $dx$ starting at $x$. Then $f(x)dx$ is the area of that infinitely thin rectangle. The integral sign is an elongated "S" that tells you to Sum the infinitely many infinitely thin rectangles to get the area.

Before you or anyone else complains that this makes no sense - I agree. But it is a very useful way to get your head around what happens when you use real rectangles and make them thinner and thinner.

Now when you do a $u$-substitution you are really using the function $u$ of $x$ to distort the $x$-axis, making it a $u$-axis instead. Substituting for $x$ in $f(x)$ tells you where to look on the $u$ axis. Changing $dx$ to $du$ takes into account the fact that your distortion stretches or shrinks the bases of the skinny rectangles. And of course you need to change the end points of the definite integral to their values on the $u$-axis.