1

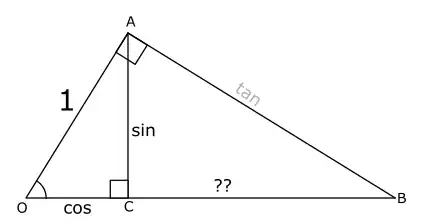
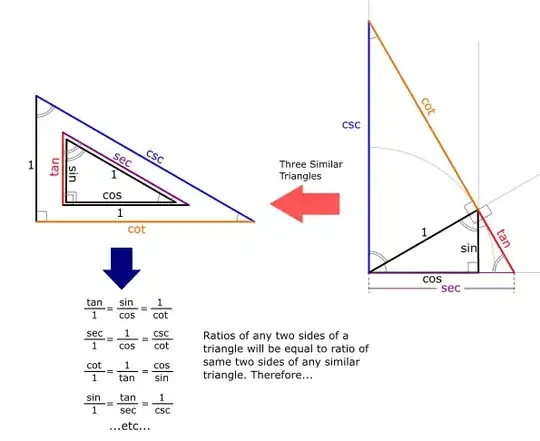
I've seen a lot of "proofs" for this - but they all somehow revolve around the definition of $tan(x)$ being $\frac{opposite}{adjacent}$. I am coming from the standpoint of being unconvinced that this is true, while looking at the following diagram:

My Right Triangle

Forgetting for a minute that $\overline{AB}$ is defined as the "tangent" - How can I geometrically prove that $\overline{AB}$ is really $\frac{opposite}{adjacent}$ or $\frac{sin}{cos}$?

I believe this would also probably not be able to avoid the fact that $\overline{OB}$ is cosecant. I likewise can't probe this (hope I can once $tan(\theta)$ is clear...

Community
  • 1
Brad
  • 133
  • 2
    Since the length of $OA$, which is the adjacent side, is $1$, we have that the length of $AB$ is trivially equal to $\frac{\text{opposite}}{\text{adjacent}}$. Besides, how can you doubt that a definition is true? I can understand doubting whether $\frac{\text{opposite}}{\text{adjacent}} = \frac\sin\cos$, and wanting a proof of that, but that's another story. – Arthur Nov 05 '18 at 15:15
  • 1
    @Brad It's opposite over adjacent, not the other way 'round. – saulspatz Nov 05 '18 at 15:24
  • 2
    Definitions are true simply by virtue of their statement. One can ask if one definition is consistent with with another set of definitions. However, one cannot prove that a single definition is true or false. – Michael McGovern Nov 05 '18 at 15:24
  • That doesn't make it any clearer - it is unproven above what $\overline{OB}$ is - so we don't know what the length of "opposite" is. – Brad Nov 05 '18 at 15:27
  • So forget about the fact that AB is tangent - just prove what length of AB is. There has to be a geometric way to probe this. To just say "it's the tangent - and the tangent is defined as follows" doesn't prove it - and is circular logic. – Brad Nov 05 '18 at 15:29
  • 1
    Well, then. By similarity of the triangles $\triangle OAB$ and $\triangle OCA$, and assuming the length of $OB$ is $1$ (as that seems like something which is given to us), the length of $AB$ is exactly $\frac\sin\cos$. – Arthur Nov 05 '18 at 15:31
  • I'm of a mind that tan is not defined as "opp/adj" or "sin/cos", but rather by a relation to an appropriate segment to the unit circle. Specifically, for the circle centered at $O$ and passing through $A$, the "tan" segment is tangent to that circle. (The name means something!) One deduces the "sin/cos" relation (and "opp/adj") via similarity: $\triangle OCA$ is similar to $\triangle OAB$, so the sides are proportional to make tan/1 = sin/cos (and sec/1 =1/cos). See my note "(Almost) Everything ... About Trig" (PDF). – Blue Nov 05 '18 at 15:31
  • @Blue, well I'm of a mind that $\sin$ and $\cos$ are defined by their power series and $\tan$ as their ratio. It's likely that there is also someone reading these comments of a mind that $\sin$ and $\cos$ are defined by appropriate differential equations. Now, being of different minds, it's not really an issue what "true" definition is, the real job is to prove that all these are equivalent. Choosing one characterization over the other is just a matter of who your audience is when you are doing the exposition of the material. Foundations have been done by great mathematicians years ago. – Ennar Nov 05 '18 at 15:57
  • @Ennar: Indeed. Incidentally, this answer of mine, and also this one, show the equivalence of the geometric and series definitions of sine, cosine, tangent, and secant. (I'm still on the hunt for cotangent and cosecant.) – Blue Nov 05 '18 at 16:10
  • 2
    Thanks all. I had completely missed that these triangles were SIMILAR (had to go prove it to myself). And that when they are - there is equivalence in side-ratios. Once I got that - it all clicked! – Brad Nov 05 '18 at 16:14

3 Answers3

2

Triangles $OAC$ and $ABC$ are similar since they have the same angles. It follows that appropriate side lengths are proportional, in particular:

$$\frac{|AB|}{|OA|} = \frac{|AC|}{|OC|} \implies \frac{|AB|}{1} = \frac{\sin x}{\cos x}\implies |AB|=\frac{\sin x}{\cos x}.$$

Ennar
  • 23,082
1

Use similarity. $\Delta OAC$ and $\Delta ABC$ are similar. When two triangles have congruent angles, then they must be similar. When this is the case, the ratio between the lengths of corresponding sides must be equivalent. Use $\angle O$ as the reference.

$$\Delta OAC \implies \frac{adjacent}{hypotenuse} = \frac{\cos O}{1}$$

$$\Delta ABC \implies \frac{adjacent}{hypotenuse} = \frac{\sin O}{\overline{AB}}$$

The two ratios must be equivalent.

$$\frac{\cos O}{1} = \frac{\sin O}{\overline{AB}}$$

$$\cos O\cdot \overline{AB} = \sin O \implies \overline{AB} = \frac{\sin O}{\cos O} \implies \overline{AB} = \tan O$$

KM101
  • 7,176
0

Not taking "credit" for the answer - but my own visual summary of the good answers provided:

enter image description here

Brad
  • 133