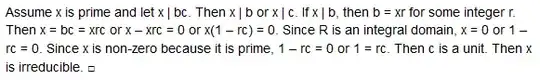I am trying to understand the proof for the following theorem:
Let $R$ be an integral domain. If $x \in R$ is prime, then $x$ is irreducible.
Here is the proof:
I typed this a while ago and I don't understand the part where if $x | bc$, then $x=bc$? Is something wrong at this step?
Also, is the definition of prime elements where $p$ is prime if whenever $p|ab$, then either $p|a$ or $p|b$? Now I don't feel so sure. This could be the reason why I am not understanding the proof...
I think you were trying to make the argument that if $x =bc$, then one of them must be a unit (and you meant $x=bc$ in your first line.)
Then, it definitly follows that $x \mid bc$, and since this is a prime, then $x \mid b$ or $x \mid c$, and the rest works.
An element is irreducible if it is not the product of two non units.
The proof must be suppose that $x$ is the product of two non units, $x=bc$, since $x$ is irreduclible, $x|b$ or $x|c$, suppose that $b=rx$, $x=rxc$ implies that $(1-rc)x=0$ since $A$ is integral, $1=rc$ and $c$ is a unit. Contradiction.
You have it reversed. What you seek is $(1)\Rightarrow(2)$ below (converse of Euclid's Lemma).
Theorem $\ (1)\,\Rightarrow\,(2)\!\iff\! (3)\ $ below, $ $ for a nonunit $\,p\neq 0\,$ in an integral domain $R$.
$(1)\ \ \ \color{#c00}{p\ \mid\ ab}\ \Rightarrow\ p\:|\:a\ \ {\rm or}\ \ p\:|\:b\quad$ [Definition of $\:p\:$ is prime]
$(2)\ \ \ \color{#c00}{p=ab}\ \Rightarrow\ p\:|\:a\ \ {\rm or}\ \ p\:|\:b\quad$ [Definition of $\:p\:$ is irreducible, in associate form]
$(3)\ \ \ p=ab\ \Rightarrow\ a\:|\:1\ \ {\rm or}\ \ b\:|\:1\quad$ [Definition of $\:p\:$ is irreducible, in $\rm\color{#0a0}{unit}$ form]
Proof $\ \ \ (1\Rightarrow 2)\,\ \ \ \color{#c00}{p = ab\, \Rightarrow\, p\mid ab}\,\stackrel{(1)}\Rightarrow\,p\mid a\:$ or $\:p\mid b.\ $ Hence prime $\Rightarrow$ irreducible.
$(2\!\!\iff\!\! 3)\ \ \ $ If $\:p = ab\:$ then $\:\dfrac{1}b = \dfrac{a}p\:$ so $\:p\:|\:a\iff b\:|\:1.\:$ Similarly $\:p\:|\:b\iff a\:|\:1.$
