I'm sure this was asked before, but I wasn't able to find the answer.
If we have an alternating series with slow convergence, can't we just use the arithmetic mean to get a much better approximation to the limit?
For example, every source says that Leibniz series for $\pi$ is a very bad way to compute it, but if we just divide the last term of a partial sum by $2$, which is equivalent to taking the arithmetic mean of consecutive partial sums, we get a faster convergence.
Have Leibniz or other researchers at the time used this method for getting a good approximation to $\pi$?
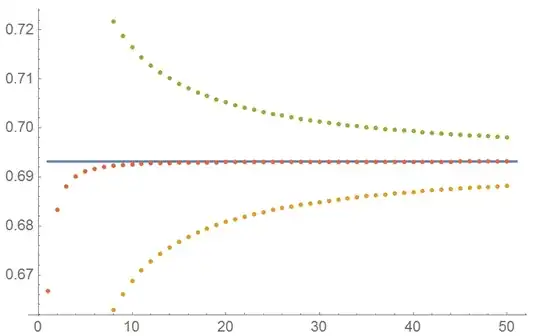
Here's the partial sums of Leibniz series (even in orange and odd in green), their arithmetic mean (red) and the exact value of $\pi/4$ (blue) plotted together:
Another example: the alternating series for $\log 2$:
There's a similar question, but it's not about history, just about the method itself: Pi series that converges arbitrarily fast.. $$ $$ Also note, that I'm not interested in more advanced methods of series acceleration, but in whether this (extremely simple and obvious one) been used at the time