0

Question

What is the asymptotic behavior of $$\sum_{n=1}^x\sigma_a(n)\sigma_b(n)$$

Where $\sigma_k=\sum_{d|n}d^k$

More generally I am curious if we can get bounds on $$\sum_{n=1}^x\prod_{i}\sigma_{k_i}(n)$$

Tools that I already have in my toolbox

I believe that $\sum_{n=1}^x \sigma_k \approx \frac{\zeta(k+1)}{k+1}x^{k+1}$

I have already encountered Abel's Summation which gives us a lot of power to make claims about the asymptotic behavior of sums.

Motivations: I would like to learn more about what tools are in the toolbox for handling $\sum AB$ when I know something about the $\sum A$ and the $\sum B$.

Some Efforts

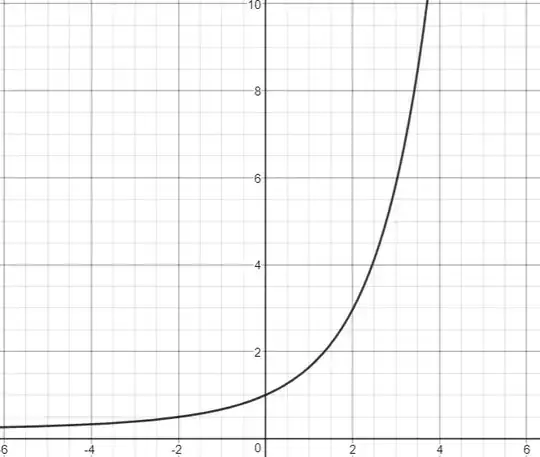
I am not sure how much help my initial efforts are in tackling the main question of this post but here they are nonetheless. These efforts are related but I am starting with the simpler case of $a=b=1$ and seeing if I can make progress on that. I have made an investigation into $\sum_{n=1}^x (\frac{\sigma_1(n)}{n})^m \approx c_m x$ where $c_m$ varies in $m$. The motivation for exploring the asymptotic behavior of this particular fraction can be seen here. You can also find that $c_1=\pi^2/6$ by reading that post. Taking $m=2,a=1,b=1$ we find that $$\sum_{n=1}^x \frac{\sigma_a(n)\sigma_b(n)}{n^m}= \sum_{n=1}^x\bigg(\frac{\sigma_1(n)}{n}\bigg)^2 \approx c_2x\approx 2.8x$$

enter image description here

Pictured in the graph above is $c_m$ on the y-axis and $m$ on the x-axis. I haven't quite figured out what this function is exactly. So this is a related unsolved puzzle for me.

Mason
  • 3,792
  • on a related note; the way to cause very large values of the summand $\sigma_a(n) \sigma_b(n)$ is to take $n= \operatorname{LCM} {1,2,3,4,..., k-1,k }$ for some integer $k > 0 ; . ; $ This follows from comments of Ramanujan on his superior highly composite numbers. Actually programming the SHC numbers is a mess, but the LCM is not so bad. – Will Jagy Oct 31 '18 at 01:52
  • 1
    Superior Highly Composite Numbers – Mason Oct 31 '18 at 01:54
  • I guess. Or consider in other ways. I have never done anything with the sums you discuss, but from Hardy and Wright I know that the extreme behavior of your function is quite different from its average behavior – Will Jagy Oct 31 '18 at 01:55
  • The other famous kind are the Colossally Abundant Numbers of Alaoglu and Erdos, about 1944. These were not included in the original Ramanujan article owing to shortages of paper; fairly recently, Nicolas and Robin published the missing material from Ramanujan (about 1915) – Will Jagy Oct 31 '18 at 01:58
  • In the Ono paper... which you suggested to me... there appears a sum of the product of sum of divisor functions. This is in corollary 2. This is in part what inspired this question. Getting some control over this type of sum could be quite a powerful tool. – Mason Oct 31 '18 at 02:01
  • 1
    Colossally Abundant Numbers – Mason Oct 31 '18 at 02:17
  • I meant for $a \ge b > 0$ then $\sum_{n \le x}\sigma_a(n)\sigma_b(n) = Res(\frac{F(s)}{s}x^s,1+a+b)+O(x^{1+c+\epsilon})$ $=\frac{G(1+a+b)}{1+a+b}x^{a+b+1}+O(x^{1+c+\epsilon})$ where $c = a+b-\min(a,1)$, $F(s) = \sum_{n=1}^\infty \sigma_a(n)\sigma_b(n) n^{-s} =\prod_p (1+\sum_{k\ge 1}\sigma_a(p^k)\sigma_b(p^k)p^{-sk}) $ $= H(s) \prod_p (1+(p^a+1)(p^b+1)p^{-sk})=G(s) \zeta(s-a-b)$ and $\log G,\log H$ converge absolutely for $\Re(s) > 1+a$. https://en.wikipedia.org/wiki/Hardy%E2%80%93Littlewood_tauberian_theorem – reuns Oct 31 '18 at 23:45

0 Answers0