The Gamma function satisfies the relation $z\Gamma(z)=\Gamma(z+1)$, whence $|\Gamma(z+1)|>|\Gamma(z)|$ whenever $|z|>1$ (and $z$ is not a non-positive integer). This naturally leads us to the idea that for a fixed $y>1$ the function $|\Gamma(x+iy)|$ of the variable $x$ could be increasing. Is this true? I would much appreciate a reference or a proof. The area $\{x+iy: \ x>1, \ y<1\}$ is of interest as well.
Asked
Active
Viewed 665 times
0
-
$$|\Gamma(x+iy)| \sim \sqrt{2 \pi} , |y|^{x-1/2} \exp{(-\frac{\pi}{2}|y|)} , \quad y \to \infty$$ can be found in Gradshteyn and Ryzhik, eq. 8.328, and a reference given therein. Eq. 8.326.2 might be of interest to you as well. – user321120 Oct 29 '18 at 18:43
-
@skbmoore: IMO your hint does not apply here, because $y$ should be fix. – gammatester Oct 29 '18 at 18:48
-
2Real and imaginary part of Gamma function. – AccidentalFourierTransform Oct 29 '18 at 18:57
1 Answers
1
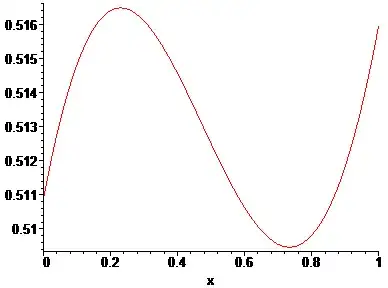
This is wrong. Here a plot for $|\Gamma(x+1.01 \cdot i)|$
$$|\Gamma(0.2+1.01\cdot i)|= 0.516403048428670750862809525289$$ $$|\Gamma(0.6+1.01\cdot i)|= 0.510624247985962860913065928364$$
gammatester
- 18,827
-
Thanks, you are right. But in fact I am interested in this property for sufficiently large $y$. What should I do then? Accept this answer and open a new question? – Durac Oct 29 '18 at 19:08
-
It is your decision. (The critical $|y|$ seems to be very close to $1$). – gammatester Oct 29 '18 at 19:14
-
https://math.stackexchange.com/questions/2976553/the-derivative-of-the-gamma-function-once-more – Durac Oct 29 '18 at 19:24
-
I'd say there is a convex curve $x+i, f(x)$ with $f(-\infty) = +\infty, f(+\infty) = 0$ such that for every $z, \Im(z) \ge f(\Re(z))$ then $|\Gamma(z+x)|$ is strictly increasing in $x > 0$. Thus a question would be the asymptotic of the optimal $f$. @Durac – reuns Oct 29 '18 at 22:07