2

This is homework assignment.

Let $(x_n)$ be bounded sequence. Prove following equation

$$\liminf_{n \rightarrow \infty}\, x_n = \max \{ B \in \mathbb{R} : \forall \varepsilon > 0 \{n \in \mathbb{N}: x_n \leq B - \varepsilon\} \; \text{is finite set} \}$$

I don't understand right side of equation, where it says that $\{ n \in \mathbb{N}: x_n \leq B - \varepsilon \}$ is finite set.

I understand concept of $\liminf_{n\rightarrow\infty}$ though.

$\liminf_{n\rightarrow\infty}\; x_n = \lim_{n\rightarrow\infty}\inf\{x_k: k \geq n\}$

user10354138
  • 33,239
flowian
  • 541

3 Answers3

2

I will not give a full proof but some insight in order to understand what it is going on and then proceed by your self to find or follow the formal proof.

Let denote as

$$L=\liminf_{n \rightarrow \infty}\, x_n\in \mathbb{R}$$

then consider

$$ B \in \mathbb{R} : \forall \varepsilon > 0 \{n \in \mathbb{N}: x_n \leq B - \varepsilon\}\; \text{is a finite set} $$

it means that $\forall \varepsilon > 0\, \exists \bar n$ such that $\forall n\ge \bar n$, that is eventually

$$x_n \geq B - \varepsilon$$

Now recall that by the definition we have also that $\forall \varepsilon > 0$

  • $x_n\ge L-\varepsilon$ eventually

  • $x_n\le L+\varepsilon$ frequently

Here is a sketch of what is going on

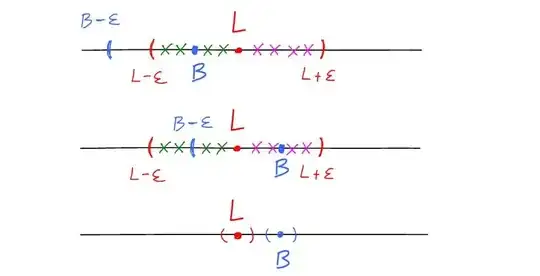
enter image description here

we can see that when $B>L$ there is some problem with the condition $x_n \geq B - \varepsilon$.

user
  • 154,566
  • Shouldn't $x_n \geq B - \varepsilon$ be $x_n > B - \varepsilon$ ?

    I haven't read further yet.

     – flowian Oct 27 '18 at 13:56
  • I think it doesn’t change anything in the argument assuming the strict inequality. – user Oct 27 '18 at 14:00
  • True, having read further, it does not. – flowian Oct 27 '18 at 14:01
  • The key point is that if $B>L$ we can find $\epsilon$ such that eventually $x_n<B-\epsilon$ that is $\epsilon<(B-L)/2$. – user Oct 27 '18 at 14:07
  • In the last part, in definition we have.

    $\liminf_{n\rightarrow\infty}x_n = L \Leftrightarrow ; \forall \varepsilon \exists N\in \mathbb{N}: n \geq N \implies |\inf_{k \geq n}x_k - L| \leq \varepsilon$.

    isn't it ?

     – flowian Oct 27 '18 at 17:02
  • It can be shown that the definition corresponds to $\forall \varepsilon > 0$ we have $x_n\ge L-\varepsilon$ eventually and $x_n\le L+\varepsilon$ frequently – user Oct 27 '18 at 18:11
1

Suppose $\{n:x_n\leq B-\epsilon\}$ is a finite set for each $\epsilon.$ Then $x_n >B-\epsilon$ for all $n$ sufficiently large which implies $\lim\inf x_n \geq B-\epsilon$ . This is true for all $\epsilon$, so $\lim\inf x_n \geq B$. This proves LHS $\geq$ RHS. On the other hand $\lim\inf x_n -\epsilon <x_k$ for all $k$ sufficiently large. If you denote $\lim\inf x_n $ by $B$ then $B-\epsilon <x_k$ for all $k$ sufficiently large. So $B$ belongs to the set in the RHS so RHS $\geq B=\lim\inf x_n $. This completes the proof. I have used two properties of $\lim\inf$:

1) if $B <lim\inf x_n$ then $B<x_n$ for all $n$ sufficiently large

2) if $x_n \geq c$ for all $n$ sufficiently large then $\lim \inf x_n \geq c$.

Kavi Rama Murthy
  • 311,013
1

On base of the definition that you are familiar with we can find:

  • If $y>\liminf_{n\to\infty} x_n$ then the set $\{n\mid x_n\leq y\}$ is infinite.

  • If $y<\liminf_{n\to\infty} x_n$ then the set $\{n\mid x_n\leq y\}$ is finite.

Now have a look at the condition:$$\{n\mid x_n\leq B-\epsilon\}\text{ is finite for every }\epsilon>0\tag1$$

The second bullet guarantees that $(1)$ is satisfied for $B=\liminf_{n\to\infty} x_n$.

If $B>\liminf_{n\to\infty} x_n$ then we can find an $\epsilon>0$ such that also $B-\epsilon>\liminf_{n\to\infty} x_n$ and then the first bullet guarantees that $(1)$ is not satisfied.

This means exactly that $\liminf_{n\to\infty} x_n$ is maximal element of the set of elements $B\in\mathbb R$ that satisfy $(1)$.

drhab
  • 151,093