1

I hope this question is not too long, but I have included some extra information to clarify the context of the question and hopefully avoid the 'circular' arguments which inevitably occur on this topic (please pardon the unavoidable pun).

In this question, by "proving $\pi$ exists" I mean proving that the limit of the following sequence $(p_{n})$ of real numbers exists, according to the familiar formal definition of sequence convergence from analysis, ie $\exists L \in \mathbb{R}$ such that $\forall \varepsilon > 0, \exists N$ such that $\forall n > N, | p_{n} - L | < \varepsilon $ :-

Firstly define $C_{n} =$ perimeter of the $n$-sided regular polygon inscribed inside the circle of radius $r$, so that (by elementary means) we have $C_{n} = 2r(n \sin \frac{SA}{n})$, and then define $p_{n} = n \sin \frac{SA}{n}$, so that $C_{n} = 2rp_{n}$, where $S\!A$ denotes a 'straight-angle'.

By "without formal analysis" I mean with only the most basic notions of limits from analysis - ie just enough for us to have a formal definition of a limit and its most basic properties (such as adding/multiplying limits and the Cauchy criteria for convergence).

Please note I have not used any angle measure in the above definition of $p_{n}$ to emphasize that the question is at the very elementary level of Geometry - with only the most basic ideas of limiting processes being used, ie. the formal definition of convergence of a sequence in $\mathbb{R}$, the basic properties of sums and products of such limits, and the Cauchy criteria for convergence (all of which are established at very early stage in real analysis). The elementary Geometry comprises the basic notions such as found in Euclid's Elements, concerning primarily straight lines and flat surfaces, but not curved objects - except for the circle, which we are just starting to consider in regard to $\pi$. This very basic Euclidean Geometry includes such things as the similar triangles, trigonometric ratios and their formulae, and lengths and areas of straight lines and polygonal regions, properties of angles in circles, and the Pythagorean Identity, and so on. It also includes $\mathbb{R}$ defined geometrically as a continuum of points using the real number line (ie 1D Euclidean Space), which is a Complete Ordered Field, containing the rational sub-field $\mathbb{Q}$. (As any two Complete Ordered Fields must be order isomorphic, analysis thus applies to this geometric 'version' of $\mathbb{R}$). This basic geometry suffices to obtain the formula for $C_{n}$ above. It does not use limiting processes except for the most basic notions mentioned above, so we can consider the present question.

In particular it does not have radian measure - and we could imagine angle $S\!A$ as belonging to a set $\mathbb{A}$ which comprises all planar angles, ie right angles, acute angles, obtuse angles, reflex angles, and so on (ie as in Euclid's Elements, which does not use any angle measure). The geometric trig functions $\sin$ and $\cos$ would then be functions from $\mathbb{A} \rightarrow \mathbb{R}$, and when an angle measure is introduced they would become functions $\mathbb{R} \rightarrow \mathbb{R}$.

The well known analysis proof of convergence of $(p_{n})$ is made by formally defining radian measure of angle and by using the power series definitions of the trig functions $s(x)$ and $c(x)$. This requires a fair bit of work in analysis - for example the theory of differentiation, integration, and power series are all needed.

[The formal definition of radian measure can be made as follows :-

  • First of all let $f(x) = \sqrt{1 - x^{2}}$ for $x \in [-1, 1]$ (ie. the upper half of the unit circle).

  • Then define the improper integral $l(x) = \int_{x}^{1} \sqrt{1 + f'(t)^2} \:dt$ (= $\int_{x}^{1} 1 / \sqrt{1 - t^2} \:dt$) for $x \in [-1, 1]$ (ie from the formal analysis definition of curve length).

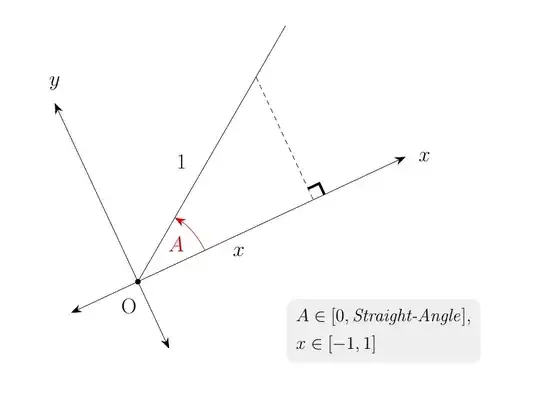
  • Then given $A \in [0, SA]$, where $SA$ denotes 'straight-angle', project a unit length of one of the sides of the angle perpendicularly down onto the other side and set up $xy$-axes as shown in the figure below. Then radian measure $m(A) := l(x)$, where $x$ = projection of this unit length onto the $x$-axis. For $A$ outside the range $[0, SA]$ we just add or subtract whole multiples of $m(SA)$ as appropriate.

enter image description here radian measure diagram

Then we would have to prove :-

  • This function $m$ is a valid definition of an angle measure (ie it is 'additive').

  • $m(SA) = 2\gamma$, where $\gamma$ is the first positive root of the function $c(x)$.

  • Wrt this angle measure we have sin/cos from Geometry equal to the analytically defined s(x)/c(x) functions.]

Then with this formal definition of radian measure we could prove $(p_{n})$ converges to the real number $2\gamma$ as follows :- \begin{eqnarray*} p_{n} & = & n \sin \left(\frac{SA}{n} \right) \\ & = & n \, s \left( m \left(\frac{SA}{n} \right) \right) \mbox{(by equivalence of $sin$ and $s$ when using radian measure $m$)} \\ & = & n \, s \left( \frac{1}{n} \; m(SA) \right) \mbox{(by multiplicative property of any angle measure)} \\ & = & n \, s \left( \frac{2\gamma}{n} \right) \mbox{(radian measure of SA is $2\gamma$)} \\ & = & 2 \gamma \: \frac{ s(2\gamma/n) }{ (2\gamma/n) } \\ & \rightarrow & 2\gamma \:\: \mathrm{as} \:\: n \rightarrow \infty \end{eqnarray*}

since $\lim_{h \rightarrow 0} s(h)/h = 1$ from analysis.

This gives a rigorous proof of the existence of $\pi$, but note there is quite a lot of analysis behind that proof.

My question is is there some elementary geometric or algebraic method of proving $lim_{n \rightarrow \infty} (p_{n})$ exists (or equivalently it is a Cauchy sequence), which does NOT require this amount of analysis, but only needs the most basic definitions of limits of sequences and their elementary properties ?

One of the motivations in asking this question is that recently I came across a proof using only elementary geometric methods of the Basel Identity, $\sum_{n = 1}^{\infty} 1/n^{2} = \pi^2/6$, which formerly I understood as only been provable using fairly complicated or advanced methods, such as the Residue Theorem in Complex Analysis. It took some years for leading mathematicians of the 1700's to obtain a rigorous proof of this identity. This elementary proof is described in this YT video, and the heuristic argument described there can readily be turned into a fully rigorous geometric proof. (Although this elementary proof does make use of some basic real analysis, it does not require anything as advanced as the Residue Theorem).

Ross Ure Anderson
  • 429
  • 2
    Your sequence is increasing and bounded above. It's pretty easy to prove that such a sequence converges. You are overcomplicating things... – Najib Idrissi Oct 26 '18 at 20:58
  • I think the interesting geometric content here is what this article calls Axiom 2 (basically, that perimeter is an increasing function for convex shapes). Since you only need the polygonal case, it's elementarily provable, and gets you boundedness and enough monotonicity to work with (specifically, that $p_n \leq p_{kn}$ for all $n,k$ with $n \geq 3$). – Micah Oct 26 '18 at 21:04
  • Didn't Archimedes use perimeters of inscribed and circumscribed polygons to find arbitrarily close bounds on the circumferance of a circle? – Somos Oct 26 '18 at 21:19
  • 1
    @Somos. If inscribed polygons with sides of 2$^n$ are used,a sequence can be constructed without using trig. – William Elliot Oct 26 '18 at 23:05
  • @Micah - a simplified form of Axiom 2, namely for a convex polygonal path inside a triangle sitting on the same base (which can be proved using induction) readily shows $C_{n}$ is bounded above by considering the bounding rectangle of $C_{n}$ which sits inside the bounding square of the circle and meets $C_{n}$ at vertices and along edges. However proving $C_{n}$ is monotone increasing (MI) is a bit trickier. You rightly say every subsequence of $C_{n}$ which starts with some index and then multiples that index successively by integers must be MI - as mult by a $k$ means the vertices (cont.) – Ross Ure Anderson Oct 27 '18 at 10:22
  • of $C_{n}$ remain in place with new ones added by replacing each side by $k$ equal sides, and the shortest path between any two vertices is the straight line. But generally a sequence $(a_{n})$ that has all such subsequences as MI is not necessarily MI itself - eg consider (2, 4, 7, 6, 2, 8, 12, 12, 12, 12, .... ). For example how could we show $p_{9256} < p_{9257}$? Analysis does though prove $C_{n}$ is MI because we can differentiate $(\sin x)/x$ and using $\tan x > x$ show it is negative on $(0, 2\gamma/3)$ (ie for $n \geq 3)$. We could just suggest defining (cont.) – Ross Ure Anderson Oct 27 '18 at 10:24
  • $\pi = \lim_{n \rightarrow \infty} (p_{2^{n}k})$, but we could just as easily define it as $\pi = \lim_{n \rightarrow \infty} (p_{3^{n}k})$ or $\pi = \lim_{n \rightarrow \infty} (p_{4^{n}k})$, etc, but we have no formal proof all these limits are equal so that is not entirely satisfactory. What we need is a way to prove $(p_{n})$ itself is convergent or MI, then all the subsequences converge to that limit also. – Ross Ure Anderson Oct 27 '18 at 10:37
  • 1
    Right, which is why I said "enough monotonicity to work with" and not actually "monotonicity". Since the sequence is bounded, you can define $\pi=\sup {p_n}$; the inequality then gives you a specific monotone subsequence which converges to $\pi$, namely $p_{n!}$. If you really want monotonicity (or even convergence) of your original sequence, you need to do some more analysis, but my approach does give a fairly natural-looking (and choice-independent) definition of $\pi$, using only elementary geometry and the least upper bound property. – Micah Oct 27 '18 at 20:07
  • @Micah - that is a good approach, and $(p_{n!})$ as the approximating sequence for $\pi$ works well, since unlike $(p_{2^{n}k})$ and so on we can easily prove it converges to $\sup {p_{n}}$. An advantage also is we now have the outer circumscribed polygons $D_{n} = 2r(n \tan (SA/n) = 2rq_{n}$ converging to this same $\pi$, for the above types of subsequences of $(q_{n})$ are monotone decreasing (MD) (by simplified Axiom 2), and we have $\inf {q_{n}} = \lim (q_{n!}) = \lim (p_{n!}) = \pi$, since $q_{n} = p_{n} / \cos(SA/n)$. So the answer (cont.) – Ross Ure Anderson Oct 28 '18 at 16:42
  • to my question is in the affirmative. I think this would be a good example to cite early on in a first course in Analysis as it gives a rigorous definition of $\pi$ from only straight-line geometry, and it replaces an 'intuitive' definition of $\pi$ with an 'a priori' one (and we do not have to wait until power series and so on have been developed). The main theorem we have used is that bounded monotone sequences converge. Convergence of $(p_{n})$ though does appear to require the extra analysis. – Ross Ure Anderson Oct 28 '18 at 16:42
  • 1
    Possibly quite relevant (if not, sorry, but I just happen to have been thinking about this recently): Does any extant Greek text prove that the area of an inscribed regular polygon increases with the number of sides?. If the area of a regular $n$-gon inscribed in a circle of radius $r$ is $\bar{p}_nr^2$, then $(\bar{p}_n)$ is strictly increasing and bounded above, for instance by $4$. – Calum Gilhooley Nov 06 '18 at 15:11
  • @Calum - proving $(A_{n})$ (and hence $(\overline{p}{n})$) is MI wouldn't immediately prove $(p{n})$ is MI as $\overline{p}{n} = p{n} \cdot \cos(SA / n)$ and $\cos (SA/n)$ is MI. – Ross Ure Anderson Nov 06 '18 at 16:36
  • Indeed not, but I wasn't suggesting that. I meant that an approach to $\pi$ via areas rather than perimeters might also avoid "formal analysis" in a way that would satisfy you. – Calum Gilhooley Nov 06 '18 at 16:53
  • I have nothing against formal analysis! What interests me here is obtaining a simpler proof of something that we have hitherto believed required more advanced methods - as with the Basel Problem I mentioned above. – Ross Ure Anderson Nov 06 '18 at 19:27
  • I wasn't suggesting that [you have anything against formal analysis], either! You made yourself clear in the question. I only wish I'd made myself clear in the comments! :) – Calum Gilhooley Nov 06 '18 at 21:22
  • 1
    In the question in History of Science and Mathematics Stack Exchange referred to above, I have incorporated the following quick proof that $A_n$ increasing implies $p_n$ increasing. Let $A_n$ be the area and $p_n$ the perimeter of a regular $n$-gon inscribed in a circle of radius $r$. If the vertices of the $(2n)$-gon are $P_0P_1P_2\cdots$, then $P_0P_2 \perp OP_1$, therefore the area of $\triangle OP_1P_2$ is $\frac{r}{2}\cdot\frac{p_n}{2n}$; but the same area is also equal to $\frac{A_{2n}}{2n}$; therefore $p_n = \frac{2A_{2n}}{r}$; and $A_{2n}$ increases with $n$, therefore so does $p_n$. – Calum Gilhooley Nov 08 '18 at 20:53
  • @Calum - I see now that $C_{n} = 2A_{2n}/r$, so I stand corrected in my comment above. However in your answer here you have effectively proven $(p_{n})$ is strictly monotone increasing, and then immediately we have $(A_{n})$ is SMI also. I posted an answer showing how your answer actually answers in the affirmative this question also. – Ross Ure Anderson Nov 26 '18 at 20:15

1 Answers1

1

This answer by user @Calum Gilhooley provides an answer to this question in the affirmative, by showing using only elementary geometry that $\sin \alpha / \sin \beta < \alpha / \beta$ for all commensurable angles $\beta < \alpha$ in the first quadrant. What is interesting about this proof is that it does not use any angle measures, it is very purely geometric - in particular it does not use radian measure (which as we saw above requires a fair bit of analysis to rigorously define). The proof can be readily extended to incommensurable angles, but we only need the commensurable case here.

Immediately from the result we obtain that $\sin x / x$ (wrt to any simple angle measure) is strictly monotone decreasing on the first quadrant for any two commensurable angles, and hence that $(p_{n})$ is strictly monotone increasing, since using degree measure :- \begin{eqnarray*} p_{n} & = & \sin (SA/n) / (1/n) \\ & = & 180 \sin (180/n) / (180/n), \forall n \ge 3 \\ \end{eqnarray*}

and $SA/n$ and $SA/n + 1$ are clearly commensurable angles.

Thus $p_{n} \rightarrow \sup \{p_{n}\}$, as $(p_{n})$ is bounded above, as discussed above in comments to the question. The only analysis needed is the definition of convergence and the supremum property - convergence of bounded monotone sequences follows immediately from the latter - we do not even require the Bolzano-Weierstrass Theorem or the Cauchy Criteria for convergence. In short only a very small amount of analysis is needed for a formal definition and proof of existence of $\pi$ within geometry.

Ross Ure Anderson
  • 429