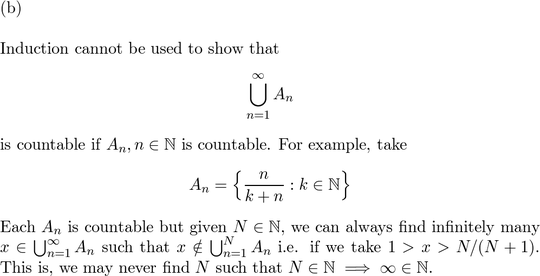4

Here is Theorem 1.5.8 in "Understanding Analysis" by S. Abbott, 2nd edition.

Theorem 1.5.8
(i) If $A_1, A_2, ..., A_n$ are each countable sets, then the union $A_1\cup A_2 \cup ... \cup A_n$ is countable.
(ii) If $A_n$ is a countable set for each $n \in \mathbb{N}$, then $\bigcup^\infty_{n=1}A_n$ is countable.

Exercise 1.5.3 (b) asks:

b) Explain why induction cannot be used to prove part (ii) of Theorem 1.5.8 from part (i).

On Slader I find this solution. I have pasted it below:

enter image description here

I don't quiet understand the reasoning above and why should it imply (does it?) that the infinite union would not be countable.

Suppose I split $\mathbb{N}$ into an infinite number of sets corresponding to the rows below:

$1 \;\;\;3 \;\;\;6 \;\;\;10\;\;...$
$2 \;\;\;5\;\;\; 9\;\;...$
$4\;\;\; 8\;\;...$
$7\;\;...$

The infinite union is clearly countable.

However, if I am to replicate the argument given in the solution, given $N\in \mathbb{N}$, we can always find infinitely many $x \in \bigcup_{n=1}^\infty A_n$ such that $x \not\in \bigcup_{n=1}^N A_n$.

What am I missing?

Andrés E. Caicedo
  • 79,201
Sandu Ursu
  • 470
  • In fact, the theorem in (ii) requires, IIRC, countable choice. – J.G. Oct 26 '18 at 19:32
  • 1
    I think this might work to illustrate as an example: Take $i \in [0,1)$, Consider a set $A_i$ such that $A_i = {i + n | n \in \mathbb{N} }$. Then suppose we have $A_i$ and $A_j$, $i \neq j$ take their intersection: $A_i \cap A_j = \varnothing$. Suppose otherwise, then $i + n = j + k$ for some $n$ and $k$. But they have the same integer part so $n = k$, but then $i + n = j + n \implies i = j$... So, consider $\bigcup_{i \in [0, 1)} A_i$, which ends up being a super set of $[0, 1)$ which is uncountable. – Dair Oct 26 '18 at 19:33
  • 1
    (Regular) induction can only tell you that something is true for each natural number. It is unable to pass into the infinite limit. To see this explicitly, try swapping "countable" with "finite", and see that the induction proof works, but the conclusion that $\bigcup_{n=1}^\infty A_n$ is finite clearly cannot be true. – Arthur Oct 26 '18 at 19:35
  • 1
    Take a look at this question about why induction can’t be used to prove properties at infinity. Among answers, there are also a lot of useful examples. – Sandro Lovnički Oct 26 '18 at 19:35
  • What this issue boils down to is this: $\infty$ is not a number, and $\infty \notin \mathbb{N}$. – Clarinetist Oct 26 '18 at 19:37
  • I sort of feel that I close this as a duplicate about once a month. – Asaf Karagila Oct 26 '18 at 19:52
  • @Arthur I understand how induction fails to cover infinity. However, isn't $\cup_{n=1}^{\infty}A_n=\cup_{n\in N}A_n$? How to differentiate the case of for all n and infinity? – Andes Lam Dec 29 '20 at 10:48
  • 1
    @AndesLam $\bigcup_{n=1}^{\infty}A_n$ is the same as $\bigcup_{n\in \Bbb N}A_n$, and standard induction can touch neither. What induction can say something about is $$\bigcup_{n=1}^kA_n=\bigcup_{n\leq k}A_n=A_1\cup A_2\cup\cdots\cup A_k$$ for any natural number $k$. – Arthur Dec 29 '20 at 11:59
  • @Arthur Is it safe to say that induction proves truthfulness of $P(n)$ for each finite natural number where as $\cup_{n=1}^{\infty}$ refers to the truthfulness of $P(n)$ for every natural number in the infinite set of natural number $N$? – Andes Lam Dec 29 '20 at 12:58
  • 1
    @AndesLam No, induction proves $P(n)$ for each finite natural number $n$, and for every natural number in the infinite set of natural numbers in the infinite set of natural numbers $\Bbb N$. That's the same thing. However, $\bigcup_{n=1}^\infty$ refers to $P(\infty)$, and $\infty$ is not a natural number, and is therefore untouched by the induction. – Arthur Dec 29 '20 at 13:06
  • @Arthur Sorry for quoting another example in the same book. In theorem 1.4.1 of Understanding Analysis, Abbott defined $I_n={x\in R: a_n\leq x\leq b_n}$ and $\exists x$ such that $x\in I_n$ for every $n\in N$. Hence, $\exists x\in\cap_{n=1}^{\infty}I_n$, Does the intersection here referring to $P(n)\forall n\in N$ or $P(\infty)$? – Andes Lam Dec 29 '20 at 13:34
  • 1
    @AndesLam There is no induction there. No $P$. Merely the definition of intersection. – Arthur Dec 29 '20 at 13:49
  • Let us continue this discussion in chat. – Andes Lam Dec 29 '20 at 14:32
  • 1
    @AndesLam No. I think it is better if you formulate your own question post. That way more people can contribute. Be sure to specify what it is you feel this question and the answers to it doesn't address. – Arthur Dec 29 '20 at 14:36

3 Answers3

4

Ignore what you found on slader -- that just doesn't make sense.

However, it is not straightforward at all to prove that you cannot use induction to prove part (ii) from part (i). Luckily, you aren't asked to provide such a proof. All you are asked to do is to give an explanation (which is much more of a pedagogical technique than it has to do with mathematics).

So, why can't you use induction here? Induction says: Suppose you have a property $P$ such that $P(0)$ holds true and $P(n) \implies P(n+1)$ for all $n \in \mathbb N$. Then $P(n)$ holds for all $n \in \mathbb N$.

In our case the property $P(n)$ is "the union of $n$ countable sets is countable". By induction we get that $P(n)$ holds true for all $n \in \mathbb N$.

The statement "the union of countable many countable sets is countable" is not among those statements $P(n)$ (there is no $n \in \mathbb N$ such that "the union of countable many countable sets is countable" is equivalent to $P(n)$). Hence induction doesn't provide us with any information about this statement.

Stefan Mesken
  • 16,651
0

First of all the statement " infinite" union of countable sets is countable is not true unless the infinite is replaced by countably infinite.

Otherwise the set of real numbers would be countable because it is an infinite union of singletons.

For your question about the induction, you can prove using induction that for every positive integer $n$ the union of $n$ countable set is countable but that is not the same thing as the union of countably infinite countable sets is countable.

Mohammad Riazi-Kermani
  • 68,728
0

The situation you are in is pretty much similar to the following:

We know that, for any $n \in \mathbb{N}$, if $r_1, \ldots, r_n$ are some real numbers, then the set $$ \left\{ r_1, \ldots, r_n \right\} = \left\{ r_1 \right\} \cup \cdots \cup \left\{ r_n \right\} $$ is a finite set.

However, if $r_1, r_2, r_3, \ldots$ are distinct real numbers, then the set $$ \bigcup_{i=1}^\infty \left\{ r_i \right\} = \left\{ r_1, r_2, r_3, \ldots \right\} $$ is NOT a finite set.

Similarly, for each $n \in \mathbb{N}$, although the set $$ \prod_{i=1}^n \{ 0, 1 \} = \underbrace{ \{0, 1 \} \times \cdots \times \{ 0, 1 \} }_{n \mbox{ times} } $$ is a countable (in fact finite) set. However, the infinite product $$ \prod_{i=1}^\infty \{ 0, 1\} = \{ 0, 1 \} \times \{ 0, 1 \} \times \{ 0, 1 \} \times \cdots $$ is not a finite (or even countable) set.

Hope you can now appreciate what is involved.

Saaqib Mahmood
  • 26,762