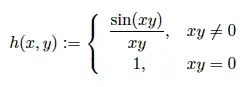5

Let $h: \mathbb{R}^2 $ -> $\mathbb{R}$

Function

I can replace $h(x, 0) = x$, so that $x=a≠0$. Then the function essentially becomes $h(y) = \frac{\sin (ay)}{ay}$. To figure out the limit for "$h(0)$", we can substitute $z = ay$: $$ \lim_{y \to 0}f(a, y) = \lim_{z \to 0}\frac{\sin z}{z} = ? $$ For $x = 0$, we have that $h(0, y) = 0$ for non-zero $y$, so $h(0, 0) = 0$ is a natural extension at the origin as well.

Is that correct, or is that wrong? Can one do this differently?

user
  • 154,566
user1234567890
  • 931
  • Why can you "replace" $h(x,0)=x$? You were given a function where $h(x,0)=1$. And why is $\lim\limits_{z\to0}\frac{\sin z}{z}=a\lim\limits_{z\to0}\frac{\sin z}{z}$? – 2'5 9'2 Oct 26 '18 at 05:00
  • 1
    Can you show $$\left|h(x,y)-1\right|\leq \frac{(xy)^2}{6}+\frac{(xy)^4}{120}$$ for any pair of $x$ and $y$? –  Oct 26 '18 at 05:18
  • By "replace", do you mean to keep the value of $x$ constant? – R zu Oct 26 '18 at 05:20
  • What if x is 0? I think just taking the limit of h as y approaches 0 is not enough. – R zu Oct 26 '18 at 05:25

4 Answers4

5

The best way to do this is to write $h$ as the composition of the maps $(x,y) \to xy$ and the map $g:\mathbb R \to \mathbb R$ defined by $g(x)=\frac {sin (x)} x$ if $x \neq 0$ and $g(0)=1$.

Kavi Rama Murthy
  • 311,013
  • 1
    The first map from x, y -> xy is continuous. The second map from z->g(z) is also continuous. Therefore, the composition x, y -> g(xy) is continuous. – R zu Oct 26 '18 at 05:36
4

Exactly the same reason with $\displaystyle\lim_{x\to0}\frac{\sin x}{x}=1$ shows that $$\lim\limits_{(x,y)\to(0,0)}\frac{\sin xy}{xy}=1$$ with the common formula $$\cos xy\leq\dfrac{\sin xy}{xy}\leq1$$ we can conclude the lmit is $1$ as the limit in one variable shows.

Nosrati
  • 29,995
2
  1. Show that for any non-zero x, as y approaches 0 from both sides ($0^{+}$ and $0^{-}$), h approaches 1.
  2. Show that for any non-zero y, as x approaches 0 from both sides ($0^{+}$ and $0^{-}$), h approaches 1.

Since approaching (0, 0) from any direction is a linear combination of just x approach 0 and just y approach 0, steps 1 and 2 show that h approaches 1 when both x and y approaches 0 from any direction. This argument is similar to a multivariable Taylor expansion of the function.

R zu
  • 697
  • 3
  • 17
0

As already noticed your claim $h(x, 0) = x $ is uncorrect since we obtain $$xy=0\cdot y=0 \implies \frac{\sin 0}{0}=1$$

to take the limit simply observe that $$(x,y) \to (0,0)\implies xy\to 0$$

then indicating $xy=z \to 0$ the limit becomes

$$\lim_{(x,y) \to (0,0)}\frac{\sin xy}{xy}=\lim_{z \to 0}\frac{\sin z}{z} = 1$$

user
  • 154,566