2

It is well known that:

$$\frac{\zeta'(s)}{\zeta(s)} + \frac{\zeta'(1-s)}{\zeta(1-s)} = \ln(2\pi) + \frac{\pi}{2}\tan\left(\frac{\pi s}{2} \right)-\Psi(s)$$

where $\Psi(s)$ is the DiGamma function.

Surprisingly, integrating the LHS and the RHS along a vertical line in the complex plane gives different outcomes. The real parts are equal, however the imaginary parts differ. For example:

$$\int_{2}^{2+100 i} \bigg(\frac{\zeta'(s)}{\zeta(s)} + \frac{\zeta'(1-s)}{\zeta(1-s)}\bigg) ds = 7.1335966...+3.137700...i$$

whereas:

$$\int_{2}^{2+100 i} \bigg(\ln(2\pi) +\frac{\pi}{2}\tan(\frac{\pi s}{2})- \Psi(s)\bigg) ds = 7.1335966...+179.074673...i$$

Q1: Why is this the case? (note: I tried different CAS tools and all yield the same difference).

EDIT 1 (based on comments): it appears that only Maple evaluates the first integral as:

$$\ln(2)-\pi i +2\ln(\pi) +\ln\big(\zeta(-1-Ti)\big)-\ln\big(\zeta(2+Ti)\big)$$

which explains the difference reported above.

I also found that the difference could be exploited to (almost) establish the number of zeros of $\zeta(s)$ with an imaginary part $< T$ through the following formula:

$$\frac{1}{2\,\pi} \Im \bigg[ \int_{2}^{2+T i} \bigg(\ln(2\pi) +\frac{\pi}{2}\tan(\frac{\pi s}{2})- \Psi(s)\bigg) ds - \int_{2}^{2+T i} \bigg(\frac{\zeta'(s)}{\zeta(s)} + \frac{\zeta'(1-s)}{\zeta(1-s)}\bigg)ds \bigg]$$

which has the closed form expression:

$$N^*(T)=\frac{1}{2\,\pi} \bigg[\Im\big(\ln\Gamma(2+iT)\big) +\pi - T\ln(2\pi) + \arg\big(\zeta(2+iT)\big)-\arg\big(\zeta(-1-iT)\big)\bigg]$$

EDIT 2: $\ln\Gamma(2+iT)$ is the LogGamma-function (i.e. LogGamma[z] in Mathematica and lnGAMMA in Maple).

When I widen the contour $-1 < \sigma > 2$ the number of zeros increases and I believe this is due to the inclusion of real (non-trivial) zeros in the count.

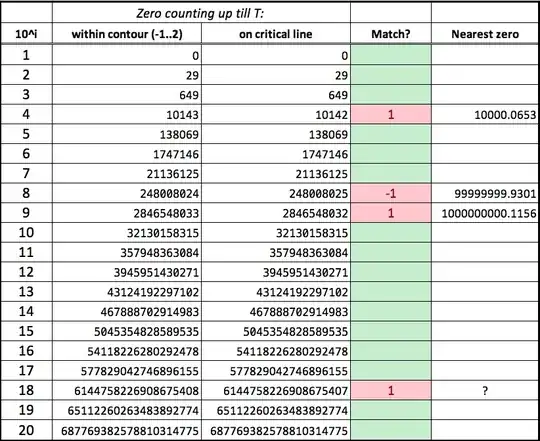
However, when I compare the number of zeros from the 'contour' with the well known formula for counting zeros on the critical line of $\zeta(s)$ up to $T$, I get the following results:

EDIT 3: I am now allowed to include pictures.

Table of zeros counted within contour and on critical line

The match between both counts seems pretty good, however occasionally could be off by $\pm 1$. This seems to occur when a non-trivial zero of $\zeta(s)$ lies very close to $T$. Therefore not sure whether I am actually counting the non-trivial zeros of $\zeta(s)$ or something 'close' to it.

Q2: Which zeros is $N^*(T)$ actually counting?

Q3: Could there be a way to select a $T$ that always gives the correct count for the zeros of $\zeta(s)$?

Rudolph
  • 21
  • 3
  • Which CAS tools did you use? Since the integrands are equal, the only possible explanation for the difference is that the integrals are being taken over different contours. $N(T)$ will measure the number of zeros of $\zeta(s)$ inside the region between these two contours, so I would assume that what is happening is the computer is taking one of the integrals along a contour that goes to the left of the critical line and the other is not. – Dark Malthorp Oct 24 '18 at 14:11
  • @DarkMalthorp I used both Maple and Mathematica. Then built the $N^*(T)$ closed form in ARB (http://arblib.org) and used it to produce the table for higher $T$. All results come out the same. I wonder whether this has something to do with the LHS of the first display having infinite 'spikes' at the non-trivial zeros that are supposed to be annihilated (i.e. the $s$ and $1-s$ components should have opposite signs in their imaginary parts)? – Rudolph Oct 24 '18 at 16:18
  • Actually, now that you mention it that is probably the answer. If numerically the poles don't quite cancel out, I suppose that could cause them to show up in the integral. (I'll admit I don't know much about numerical methods but it sounds plausible to me) – Dark Malthorp Oct 24 '18 at 18:26
  • Your first equality is of meromorphic functions, so there is no problem of branches and their integral on the same curve is equal. Now if you replace the first integral by something in term of $\Im (\log \zeta(s))$ then you need to be careful with the branches. – reuns Oct 24 '18 at 18:29
  • @DarkMalthorp it seems to be more subtle. I just tried the integrals in pari/gp and they both give exactly the same outcome (note: numeric integration). I guess Maple and Mathematica try an analytic approach to solve the integrals and then branch cuts (as user reuns suggests) will play a role and a different contour could be followed. Independently of what causes the integrals to differ (Q1), I am still keen to understand what the closed form formula for $N^*(T)$ is actually counting (Q2). – Rudolph Oct 24 '18 at 21:32
  • I just tried it in Mathematica and the integrals give the same value. – eyeballfrog Oct 24 '18 at 22:42
  • @eyeballfrog You are correct. I had accidentally used the closed form output of Maple for the integral of the LHS of the top display and evaluated that in WolframAlpha (Mathematica). Sorry for this and thanks for spotting. It now appears that Maple is the CAS producing the 'wrong' result (i.e. by producing a closed form of the integral containing logs). It is becoming more and more clear that it is the branch cut of the logs that causes the difference. Note that a similar effect happens in the evaluation of $\ln(\Gamma(2+iT))$ in the $N^*(T)$ formula. Maple evaluates differently from pari/gp. – Rudolph Oct 24 '18 at 23:02
  • What $\Im (\log \zeta(s))$ (and other functions) are counting is explained here, that is you should compare your branch of $\log \zeta(s)$ with the one which is analytic on horitonal lines and $\Re(s) > 1$ and real postive on $s > 1$ – reuns Oct 25 '18 at 09:32
  • @reuns Thanks. I found an even better explanation here: https://math.stackexchange.com/questions/1903742/testing-zeros-of-the-riemann-hypothesis/1903768#1903768 ;) – Rudolph Oct 25 '18 at 11:55

0 Answers0