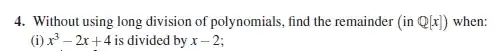Find the remainder without using long division

Question

So I was looking at other posts related to this, and most of them contained polynomials divided by a function with multiple roots. In my question, I only have $g(x) = (x-2)$, assuming $f(x) = x^{3} - 2x + 4 $. So I set it up as such:

$$f(x) = q(x)(x-2) + l(x)$$

where $l(x) = (ax+b)$

And now if I plug in $x=2$ I get $f(x) = 2a+b$ but I'm not sure where to go from here because I only have 1 unknown, and can't solve for $a$ or $b$...

score 1 · Answer 1 · answered Oct 23 '18 at 17:58

1

The remainder is a constant polynomial $k$. And if$$x^3-2x+4=(x^2+ax+b)(x-2)+k,$$then, putting $x=2$, this becomes $8=0+k$. Therefore, the remainder is the constant polynomial $8$.

answered Oct 23 '18 at 17:58

José Carlos Santos

427,504

I'm not sure where you received $x^2 + ax + b$ from? – Stuy Oct 23 '18 at 18:02
It's the quotient. For every division there is a quotient and there is a remainder, right?! – José Carlos Santos Oct 23 '18 at 18:03
Right, I'm just confused how you got that exact form. – Stuy Oct 23 '18 at 18:03
The only other thing that I used was that the degree of the remainder had to be smaller than the degree of the divisor ($x-2$). – José Carlos Santos Oct 23 '18 at 18:05
So let's say if I was doing $x^4 -7x^2 + 3 $ is divided by $x+1$, I would write it in the form: $(x^3 + ax^2 + bx + c)(x+1) + k$? – Stuy Oct 23 '18 at 18:07
Yes, you got it! – José Carlos Santos Oct 23 '18 at 18:08

Bill Dubuque · Answer 2 · 2023-11-19T23:38:50.553

Division $\:\!\Rightarrow\:\! f(x) = q(x)(x\!-\!2) + r(x),\ \bbox[5px,border:1px solid red] {\deg r < \deg(x\!-\!2) = 1}\,$ $\,\Rightarrow\,r(x) = r\,$ is constant

Hence: $\,\ \ r = f(2) = f(x)\bmod (x\!-\!2)\,$ follows by evaluating above at $\, x=2$.

Generally: $\,\ f(a) = f(x)\bmod (x\!-\!a),\, $ the ubiquitous Polynomial Remainder Theorem.

Alternatively we can use modular arithmetic for the proof:

$\!\bmod x\!-\!a\!:\,\ x\equiv a\,\Rightarrow\,f(x)\equiv f(a)\ $ by the Polynomial Congruence Rule

Find the remainder without using long division

2 Answers2