8

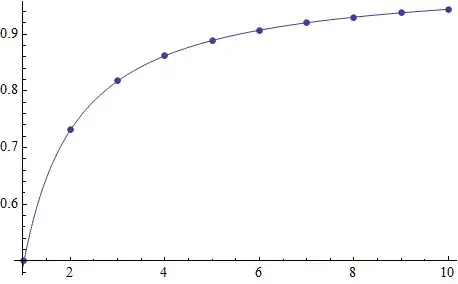
I'm looking for the solution $x$ of

$$x^n+nx-n=0.$$

Thoughts: From graphing it for several $n$ it seems there is always a solution in the interval $[\tfrac{1}{2},1)$. For $n=1$, the solution is the fraction $\tfrac{1}{2}$ and for higher $n$, the solution shifts to the right.

I then saw that the equation reads $$F_n(x)=x$$ with

$$F:[0,1]\to[0,1],\ \ \ \ \ \ F_n(x):=1-\frac{x^n}{n}.$$

I think I got all conditions together for making the iteration of $F_n$'s the general soluton for the equation. I computed $$x_5=F_5(F_5(F_5(F_5(F_5(F_5(F_5(F_5(x_S)))))))),$$

with starting value $x_S=\tfrac{1}{2}$ and it seems to be the solution of the equation for $n=5$.

Related wikipedia links: Fixed point theorem, Banach fixed-point theorem, Fixed point iteration;

I wonder:

Have I found the soluton and can one evaluate the iteration to a closed form?

Might be that it involves polylogs. edit: At least Wolfram Alpha claims to know $$n(x)=W\left(\frac{-\log(x)}{x-1}\right)/\log(x),$$ even if $n(x)$ isn't too interesting.

In my case, how is the relation between the function $x(n)$ and (I think) the fixed point combinator for the iteration?

Does it matter what I choose for $x_S$ here? Can one relate it's value and the number for necessary iteration for a good agreement with the real value?

(Also, are there any results on which polynomial equations this technique works? The property $F:[0,1]\to[0,1]$ seemed accidental to me.)

Community
  • 1
Nikolaj-K
  • 12,249
  • A related problem. – Mhenni Benghorbal Feb 06 '13 at 13:07
  • 4
    @Nick Kidman: Not a solution, but a remark: the fact that there is always a solution on $(1/2,1)$ for $n>1$ follows directly from the fact that $f_n(1/2)=1/2^n+n/2-n=1/2^n-n/2<0$ and $f_n(1)=1+n-n=1>0$. So, by the intermediate value theorem, there exists $c\in(1/2,1)$ such that $f_n(c)=0$. – Dennis Gulko Feb 06 '13 at 13:07
  • It seems like you want to do something like Newton Raphson (or root approximation). Note that for $n=1$, you will not converge towards a solution if you use any starting value that is not $x_S = \frac {1}{2}$. – Calvin Lin Feb 06 '13 at 13:25

2 Answers2

1

You can get a good approximation of the solution as $n \to \infty$ by supposing that $x$ can be written as an asymptotic series in powers of $1/n$, say

$$ x \sim 1 + \sum_{k=1}^{\infty} \frac{a_k}{n^k}, $$

then substituting this into the given equation and calculating the coefficients recursively. For example we can calculate $a_1$ and $a_2$ by writing

$$ \begin{align*} 0 &\approx \left(1 + \frac{a_1}{n} + \frac{a_2}{n^2}\right)^n + n\left(1+\frac{a_1}{n} + \frac{a_2}{n^2}\right) - n \\ &= \left(1 + \frac{a_1}{n} + \frac{a_2}{n^2}\right)^n + a_1 + \frac{a_2}{n} \\ &= a_1 + e^{a_1} + \frac{2a_2 (1+e^{a_1}) - a_1^2 e^{a_1}}{2n} + O\left(\frac{1}{n^2}\right). \end{align*} $$

By sending $n \to \infty$ we get that $a_1 + e^{a_1} = 0$ and so

$$ a_1 = -W(1), $$

where $W$ is the Lambert W function.

Then, setting the coefficient of $1/n$ to $0$ and substituting the above value of $a_1$ we find that

$$ a_2 = \frac{W(1)^3}{2(1+W(1))}. $$

Thus we have

$$ x \approx 1 - W(1) n^{-1} + \frac{W(1)^3}{2(1+W(1))} n^{-2}. $$

This approximation seems to be pretty good. Below is a plot which compares the numerical roots with the asymptotic formula for $1 \leq n \leq 10$.

enter image description here

This series might actually converge for large enough $n$ but I don't see how to prove it. If the implicit function theorem could be employed then you would be set.

Antonio Vargas
  • 24,993
0

Isn't this simply the result of the Banach fixed-point theorem? In you case one must prove that there exists $q$ such that: $$d(F_n(x),F_n(y))=\frac{|y^n-x^n|}{n} \le q |x-y|$$ Which is true for all $n>1, x>0$, with say, $q=0.9$, So that it doesn't matter what $x_S$ you choose.

Regarding a closed form - convergence of an iterative series says nothing about the existence of such a closed form solution.

Nathaniel Bubis
  • 33,018
  • Yes, I obtained the solution that way, I haven't used that before though and so I wasn't sure, especially since I solved all $n$ equations simultaneously and I couldn't find an explicit reference regarding the value of starting values $x_S$. I added some references in the quation now too. / "Convergence of an iterative series says nothing about the existence of such a closed form solution." - well yes, that's why I'm asking for this specifc example :) Wolfram Alpha computes $n(x)$ explicitly in terms of polylogs but $n$ in terms of $x$ is some kind of useless and I don't know hot to invert it. – Nikolaj-K Feb 06 '13 at 13:51
  • @NickKidman - if you knew that, what makes you think that your iterative series has anything to do with a closed form solution? the question should be re-titled "does a closed form solution for equation X exist". – Nathaniel Bubis Feb 06 '13 at 13:55
  • I now added a remark why I think one might exist in the comment above. That's also why I wrote about polylogs in the question, I though it was long enough already. – Nikolaj-K Feb 06 '13 at 13:56