Let $f_n(x)$ be the triangle function of height $1$ and width $2$, centred on $x=n$. This is what $f_6$ looks like:
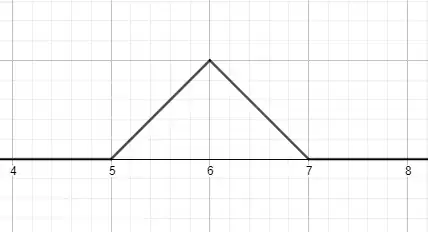
Then
- $\int_{-\infty}^\infty f_n(x)\,dx=1$ for all $n$
- $\lim_{n\rightarrow\infty}f_n(x)=0$ for all $x$
So $$0=\int_{-\infty}^\infty \lim_{n\rightarrow\infty}f_n(x)\,dx\ne \lim_{n\rightarrow\infty}\int_{-\infty}^\infty f_n(x)\,dx=1$$
Edited to add: I see now that you asked for a series, not a sequence. So replace the sequence $(f_n)$ in the above with the series $\sum g_n$, defined by $g_1=f_1$ and $g_{n+1}=f_{n+1}-f_n$. Now $\sum_{r=1}^n g_r=f_n$.
