Counting strings containing specified appearances of words

Question

Is there a nice formula (or generating function) for the number of binary strings of length $n$ that contain exactly $k$ appearances of a specified word $w$? For instance, among the binary strings of length 7, exactly fifteen contain exactly two appearances of ${101}$, namely: $$ \begin{array}{llll} 0\color{red}{101}\color{blue}{101}&1\color{red}{101}\color{blue}{101}&\\ \color{red}{101}\color{blue}{101}0&\color{red}{101}\color{blue}{101}1&\\ \color{red}{101}1\color{blue}{101}&&\\ 00\color{red}{101}\color{blue}{01}&01\color{red}{101}\color{blue}{01}&11\color{red}{101}\color{blue}{01}\\ \color{red}{101}\color{blue}{01}00&\color{red}{101}\color{blue}{01}10&\color{red}{101}\color{blue}{01}11\\ 0\color{red}{101}\color{blue}{01}0&0\color{red}{101}\color{blue}{01}1&1\color{red}{101}\color{blue}{01}0&1\color{red}{101}\color{blue}{01}1\\ \end{array} $$

In Wilf's Generatingfunctionology (section 4.12) there's a very special case of this where $k=0$ and $w=\mathtt{111...1}$. Even this example is somewhat involved, but maybe the general case isn't too much more difficult.

Answer 1

Here's a quick explanation of the Goulden-Jackson cluster method as it applies to this problem. Define a marked word to be a word with certain subwords and their location in the word marked. I'll illustrate this by parenthesizing certain subwords, with colors to indicate how the parens are matched. For example,

$$\color{red}(\text{S}\color{green}(TU\color{green})\color{blue}(F\color{red})F\color{blue}).$$

Given a set of "bad" words $B$, with no bad word contained in another, define a cluster to be a marked word so that each marked subword is in $B$, and the marked subwords overlap in such a way that the word is not the concatenation of two nonempty marked words. For example, if $B = \{AAA, AB\}$ then

$$\color{red}(AA\color{blue}(A\color{red})B\color{blue})$$ is a cluster but $$\color{red}(AAA\color{red})\color{blue}(AB\color{blue})$$ is not since the marked words don't overlap.

Now let $\mathcal{C}$ be the set of clusters, and let $\mathcal{C}(x,y)$ be the generating function $\sum_{C \in \mathcal{C}} (y-1)^{m(C)} x^{n(C)}$ where $n(W)$ is the length of the marked word $C$ and $m(C)$ is the number of marked subwords. Suppose these words are made from letters in a alphabet $S$ of size $k$, and for a word $W$ on $S$ define the weight of $W$ to be $w(W) = x^n y^b$ where $n$ is the length of $W$ and $b$ is the number of occurrences of bad words. Then the beautiful fact is

$$\sum_W w(W) = \frac{1}{1 - kx - \mathcal{C}(x,y)}$$

where the sum is taken over all words $W$ on the alphabet $S$.

The article I linked describes an algorithm to find an expression for $\mathcal{C}(x,y)$ as a rational function using linear algebra, but in this case we can find it by hand. Letting $B = \{101\}$, we see that the only possible clusters are

$$\color{red}(101\color{red}), \color{red}(10\color{blue}(1\color{red})01\color{red}), \color{red}(10\color{blue}(1\color{red})0\color{green}(1\color{blue})01\color{green}), \ldots$$

with each appearance of $101$ marked. The word in this list with $m$ occurrences of $101$ will have length $2m+1$, so

\begin{align*} \mathcal{C}(x,y) &= \sum_{m=1}^\infty (y-1)^mx^{2m+1}\\ &= x\sum_{m=1}^\infty (x^2 (y-1) )^m\\ &= \frac{x^3(y-1)}{1 - x^2 (y-1)}\\ \end{align*}

and so the desired generating function is

$$\sum_W w(W) = \frac{1}{1 - 2x - \frac{x^3(y-1)}{1 - x^2 (y-1)}}.$$

You can check that the coefficient of $x^7y^2$ is $15$, representing the $15$ binary words of length $7$ that contain two copies of $101$. Note that if we set $y=0$ we get the generating function for words that avoid $101$.

I recommend reading the above article for the details, the proofs are not too complicated.

Answer 2

Here is a series of links that document the technique.

• Systems of generating functions, section 11.1
• Good introduction to rational generating functions
• Excellent explanation of transfer matrix method
• This has the transfer matrix formulas and a bibliography.

If there are specific questions concerning the algorithm or what my Maple program does then I will answer them in the comments. I am essentially using the transfer matrix without constructing it as such in order to obtain conditional ordinary generating functions for the distribution of word ocurrences after $n$ steps for each state of the DFA, which correspond to the prefixes of $w$ (including $w$), where the coefficient of $[z^n]$ contains the exact distribution of occurrences given that the DFA was in that state after $n$ steps. Sum these to get the GF of all ocurrences after $n$ steps no matter what the last state was. Transitions from one state to another occur if the prefix corresponding to the target is the longest such prefix contained in the prefix of the current state with the transition letter appended, starting from the right of the source with the transition appended. E.g. if the word $w$ is $101$, the possible prefixes are $\epsilon, 1, 10$ and $101.$ Compute the transtions between states using the maximum prefix length rule. Pick up a $z$ for every transition and a $uz$ for transitions to $101$, to account for the fact that we have seen an ocurrence of $w$. For example, if you are at $101$ on $0$ you transition to $10$ and on $1$, to $1$.

Answer 3

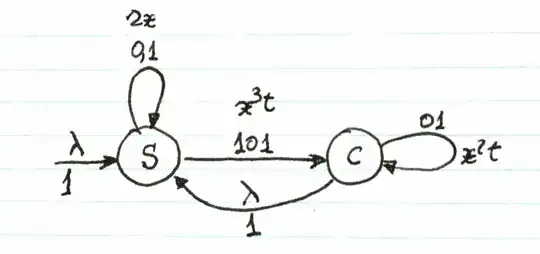
Here is an observation. While I am certain that the above advanced treatment deserves prominence, I would like to point out that one can get good results (bivariate generating functions) simply by analysing a minimal automaton with the prefixes of $w$ as states and computing the transitions from one prefix to another so that the maximum prefix is chosen at every step, and thereafter solving the resulting system of probability generating functions. Very simple indeed. The generating functions are in $z$ and $u$ where $z$ indexes the length of the string and $u$ the number of occurrences of $w.$ These yield conditional results, i.e. the PGF for a certain state gives the probability distribution of ocurrences of $w$ as a polynomial in $u$ (which is the coefficient of $z^n$ of the PGF) given that the automaton is in that state. To get all occurrences, sum the PGFs for all states and extract coefficients.

The example has $w=101$, giving generating functions $$\begin{align} a & =-2\,{\frac {{z}^{2}u+2\,z-4}{8-8\,z-2\,{z}^{2}u+{z}^{3}u+2\,{z}^{2}-{z}^ {3}}},\\ a_1 & =-{\frac { \left( -4+{z}^{2}u \right) z}{8-8\,z-2\,{z}^{2}u+{z}^{3}u+ 2\,{z}^{2}-{z}^{3}}}\\ a_{10} & =2\,{\frac {{z}^{2}}{8-8\,z-2\,{z}^{2}u+{z}^{3}u+2\,{ z}^{2}-{z}^{3}}}\\ a_{101} & ={\frac {{z}^{3}u}{8-8\,z-2\,{z}^{2}u+{z}^{3}u+2\,{z}^{2}-{z}^{3}}} \end{align}$$ Add these and simplify to obtain $$ g(z, u) = -2\,{\frac {{z}^{2}u-4-{z}^{2}}{8-8\,z-2\,{z}^{2}u+{z}^{3}u+2\,{z}^{2}-{z}^{3}}}.$$ Finally extract the coefficient of $[u^2]$, getting $$ [u^2] g(z, u) = 8\,{\frac {{z}^{5} \left( -2+z \right) }{ \left( -8+8\,z-2\,{z}^{2}+{z}^{3}\right) ^{3}}}.$$ Now the coefficients (times $2^n$ because we have a PGF) of this last term are (starting from $n=5$) $$1, 5, 15, 38, 91, 210, 468, 1014, 2151, 4487, 9229, 18756, 37728, 75219, 148803, 292354,$$ and there are indeed fifteen of these for $n=7$.

Let's treat another example, taking $w=1111.$ We get the following set of PGFs: $$\begin{align} a & =-8\,{\frac {-2+uz}{16-8\,uz-8\,z+4\,{z}^{2}u-4\,{z}^{2}+2\,{z}^{3}u-2\,{ z}^{3}+{z}^{4}u-{z}^{4}}}\\ a_{1} & =-4\,{\frac {z \left( -2+uz \right) }{16-8\,uz-8 \,z+4\,{z}^{2}u-4\,{z}^{2}+2\,{z}^{3}u-2\,{z}^{3}+{z}^{4}u-{z}^{4}}}\\ a_{11} & =-2\, {\frac {{z}^{2} \left( -2+uz \right) }{16-8\,uz-8\,z+4\,{z}^{2}u-4\,{z}^{2}+2\,{z}^ {3}u-2\,{z}^{3}+{z}^{4}u-{z}^{4}}}\\ a_{111} & =-{\frac {{z}^{3} \left( -2+uz \right) }{16-8\,uz-8\,z+4\,{z}^{2}u-4\,{z}^{2}+2\,{z}^{3}u-2\,{z}^{3}+{z}^{4}u-{z} ^{4}}}\\ a_{1111} & ={\frac {{z}^{4}u}{16-8\,uz-8\,z+4\,{z}^{2}u-4\,{z}^{2}+2\,{z}^{3 }u-2\,{z}^{3}+{z}^{4}u-{z}^{4}}} \end{align}$$ Add and simplify to get $$ g(z,u) = -2\,{\frac {-8+4\,uz-4\,z+2\,{z}^{2}u-2\,{z}^{2}+{z}^{3}u-{z}^{3}}{16-8\,uz-8\,z+4\,{z}^{2}u-4\,{z}^{2}+2\,{z}^{3}u-2\,{z}^{3}+{z}^{4}u-{z}^{4}}}. $$ Now suppose we wanted the count with four ocurrences of $w$ which has PGF $$ [u^4] g(z,u) = 16\,{\frac {{z}^{7} \left( -8+4\,z+2\,{z}^{2}+{z}^{3} \right) ^{3}}{ \left( -16+8\, z+4\,{z}^{2}+2\,{z}^{3}+{z}^{4} \right) ^{5}}}.$$ Clearly we need at least seven bits, and indeed the sequence (times $2^n$ because we have a PGF) of the coefficients of this last term is (starting from $n=7$) $$ 1, 2, 5, 12, 31, 71, 163, 369, 829, 1835, 4032, 8795, 19064, 41081.$$

I am posting the Maple code that I used to compute these and the reader is invited to try it out by invoking the function "eqsys" with a list of bits (the word $w$).

Here is a challenge for the reader: verify independently that the cumulative PGF for $w=10101$ is given by $$ g(z, u) = -2\,{\frac {4\,{z}^{2}u-16-4\,{z}^{2}+{z}^{4}u-{z}^{4}}{8\,{z}^{3}u-32\,z-8\,{z}^{2 }u+32-8\,{z}^{3}-2\,{z}^{4}u+8\,{z}^{2}+2\,{z}^{4}-{z}^{5}+{z}^{5}u}}.$$

This is the Maple code:

prfx :=
proc(w, ww)
        local pos, s1, s2;

        for pos from nops(ww) to 1 by -1 do
            s1 := cat(seq(w[k], k=1..pos));
            s2 := cat(seq(ww[k], k=nops(ww)-pos+1..nops(ww)));

            if s1=s2 then return s1; fi;
        od;

        return "";
end;

eqsys :=
proc(w)
        local mx, prf, ww, ww_name, sysl, eq, eqs_tbl;

        sysl := [];

        for mx from 0 to nops(w)-1 do
            ww := [seq(w[k], k=1..mx), 0];
            ww_name := cat(`a`, seq(ww[k], k=1..nops(ww)-1));
            prf := cat(`a`, prfx(w, ww));

            sysl := [op(sysl), [prf, ww_name, 0]];

            ww := [seq(w[k], k=1..mx), 1];
            ww_name := cat(`a`, seq(ww[k], k=1..nops(ww)-1));
            prf := cat(`a`, prfx(w, ww));

            sysl := [op(sysl), [prf, ww_name, 1]];
        od;

        ww := [seq(w[k], k=2..nops(w)), 0];
        ww_name := cat(`a`, seq(w[k], k=1..nops(w)));
        prf := cat(`a`, prfx(w, ww));

        sysl := [op(sysl), [prf, ww_name, 0]];

        ww := [seq(w[k], k=2..nops(w)), 1];
        ww_name := cat(`a`, seq(w[k], k=1..nops(w)));
        prf := cat(`a`, prfx(w, ww));

        sysl := [op(sysl), [prf, ww_name, 1]];

        print(sysl);

        eqs_tbl := table();
        for v in indets(sysl) do
            if v = `a` then
               eqs_tbl[v] := 1;
            else
               eqs_tbl[v] := 0;
            fi;
        od;

        ww_name = cat(`a`, seq(w[k], k=1..nops(w)));

        for eq in sysl do
            if eq[1] = ww_name then
               eqs_tbl[eq[1]] :=
               eqs_tbl[eq[1]] + 1/2*u*z*eq[2];
            else
               eqs_tbl[eq[1]] :=
               eqs_tbl[eq[1]] + 1/2*z*eq[2];
            fi;
        od;

        sysl := [];
        for eq in [indices(eqs_tbl, 'nolist')] do
            sysl := [op(sysl), eq = eqs_tbl[eq]];
        od;

        print(sysl);

        solve(sysl, indets(sysl) minus {u,z});
end;

Answer 4

I have studied for a while the Goulden-Jackson method and I find it kind of bully.

Imagine there is a soup S and here comes a guy throwing a potato 101 in the soup. "Fellows, there is at least one potato in the soup !" says, then he throws another potato in the soup. "Fellows, there are at least two potatoes in the soup" ! Then he applies the inclusion-exclusion principle $N(t)= E(t+1)$ and he gets the exact potatoes amount there were in the soup.

The generating functions for the language of the above automaton is given by solving.

$S = 2xS+C+1$

$C = x^3tS + x^2tC $

Here, the power of $x$ counts the length of a word and the power of $t$ the number of added 101's

The "at least" generating function is

$N(x,t) = S(x,t) = {1-tx^2 \over 1-2x-x^2t+x^3t} $

The "exact" generating function is

$E(x,t) = N(x,t-1)= {1+x^2-tx^2 \over 1-2x+ x^2 -x^3 -x^2t - x^3t} $

Answer 5

For the problem of zero ocurrences of $q$ ones I get the following PGFs:$$\begin{align} g_1 = & -2\, \left( -2+z \right) ^{-1} \\ g_2 = & -2\,{\frac {-2-z}{4-2\,z-{z}^{2}}} \\ g_3 = & -2\,{\frac {-4-2\,z-{z}^{2}}{8-4\,z-2\,{z}^{2}-{z}^{3}}} \\ g_4 = & -2\,{\frac {-8-4\,z-2\,{z}^{2}-{z}^{3}}{16-8\,z-4\,{z}^{2}-2\,{z}^{3}-{z}^{4}}} \\ g_5 = & -2\,{\frac {-16-8\,z-4\,{z}^{2}-2\,{z}^{3}-{z}^{4}}{32-16\,z-8\,{z}^{2}-4\,{z}^{3}- 2\,{z}^{4}-{z}^{5}}}\end{align}.$$

The Maple code for this goes as follows:

ones :=
proc(n)
        local sol, states, s;

        sol := eqsys([seq(1, k=1..n)]);

        states := convert(indets(sol) minus {u, z}, list);

        s := `+`(seq(states[k], k=1..nops(states)));
        factor(subs(sol, s));
end;

These value for $q=1$ is ${2}^{-n}$, which is obviously correct. Multiply by $2^n$ to compensate for the PGF and get $1$, and there is indeed just one string that does not contain the word $1$, which is a string of zeroes.

Answer 6

After working through some of the material from Jair it became obvious to me that nothing is gained by those probability generating functions, it just clutters up the output with predictable coefficients, so one should definitely use ordinary generating functions instead.

The following DIFF shows how to edit the Maple code to switch from PGFs to OGFs.

63c63
<                eqs_tbl[eq[1]] + 1/2*u*z*eq[2];
---
>                eqs_tbl[eq[1]] + u*z*eq[2];
66c66
<                eqs_tbl[eq[1]] + 1/2*z*eq[2];
---
>                eqs_tbl[eq[1]] + z*eq[2];

With these new settings the challenge function for $10101$ becomes $$ g(z,u) = -{\frac {{z}^{2}u-1-{z}^{2}+{z}^{4}u-{z}^{4}}{1-{z}^{2}u-2\,z+2\,{z}^{3}u-2\,{z}^{3}+{z}^{2}-{z}^{4}u+{z}^{4}-{z}^{5}+{z}^{5}u}}.$$

The challenge for $101010$ becomes $$ g(z,u) = {\frac {{z}^{2}u-1-{z}^{2}+{z}^{4}u-{z}^{4}}{2\,{z}^{5}-1+{z}^{2}u+2\,z-2\,{z}^{3}u+2\,{z}^{3}-2\,{z}^{5}u-{z}^{6}-{z}^{2}+{z}^{4}u-{z}^{4}+{z}^{6}u}}.$$