In the ring of residue classes modulo 20, the book says that the greatest common divisor of residue classes $9$ and $18$ is $9$. But I am getting $1,3,7,9,11,13,17,19$ .
Asked
Active
Viewed 173 times
2
-
$1,3,7,9,11,13,17,19$ are all residues that are coprime to $20$. – Eleven-Eleven Oct 15 '18 at 14:11
-
You mean all co-prime residue classes are GCDs? – Anuj Oct 15 '18 at 14:13
-
No, $(1,20)=(3,20)=...=(19,20)=1$. $(9,18)=9$ – Eleven-Eleven Oct 15 '18 at 14:17
-
But how come $(9,18)$ is not 1. $1|9$ and $9|1$ -> $1$ and $9$ are associates -> If $9$ is the gcd, then so is $1$. Same is true for all numbers I'm getting as answer. What's wrong with my argument? – Anuj Oct 15 '18 at 14:22
-
the residue class of 18 is the same as the residue class of 2 times the residue class of 9. Both residue classes are thus multiples of the residue class of 9. The idea is the same for integers..... – Eleven-Eleven Oct 15 '18 at 14:23
-
1Correct. So the gcd is not just $9$ but all the above listed integers. Right? – Anuj Oct 15 '18 at 14:26
-
GCD is defined only up to unit(invertible) factors, so gcd $\sim unit \iff $ gcd $\sim 1.,$ See here for further discussion. – Bill Dubuque Oct 15 '18 at 14:32
-
I made an error in the previous comment. I meant " So the gcd is not just residue class of $9$ but all the above listed residue classes, Right?" – Anuj Oct 15 '18 at 14:39
-
@Anuj what text are you using? – Eleven-Eleven Oct 15 '18 at 15:01
1 Answers
1
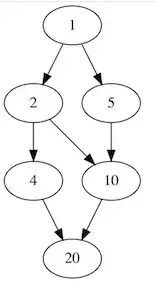
This is the divisibility graph of the classes, where $a\to b$ means $a|b$.
We don't have to list all the associates, which are in these collections:
$\{1,3,7,9,11,13,17,19\}$
$\{2,6,14,18\}$
$\{4,12,8,16\}$
$\{5,15\}$
$\{10\}$
As far as divisibility is concerned, we don't need to distinguish among associates.
Because of the direction I happened to draw my graph, the GCD's are actually the lowest thing on top of the two given elements. $9$ and $18$ correspond to $1$ and $2$ respectively, so $1$ is the greatest common divisor. This makes sense since $1$ and $9$ are already units.
rschwieb
- 153,510
-
So the $(9,18)$ is any residue class present in equivalence class of $9$, right? – Anuj Oct 15 '18 at 14:36
-
1@Anuj Yes, if by "equivalence class" you're referring to the divisibility class, not the class of integers mod $20$. – rschwieb Oct 15 '18 at 14:40