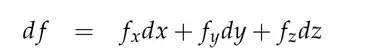Note: This answer is mainly based upon Introduction to Calculus and Analysis I by R. Courant and F. John.
We start with the single-variable case and consider a function $y=f(x)$. We will see that it is also quite standard to treat $dx$ and $dy$ as separate quantities provided we use the appropriate settings.
Definition of derivative
The definition of the derivative appears in several different forms, using the notation of Lagrange $y^{\prime}=f^{\prime}(x)$ we write
\begin{align*}
f^{\prime}(x)=\lim_{x_1\to x}\frac{f(x_1)-f(x)}{x_1-x}=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}
\end{align*}
Using the notation of Leibniz we write
\begin{align*}
\frac{dy}{dx}=\frac{df(x)}{dx}=f^{\prime}(x)=\lim_{x_1\to x}\frac{f(x_1)-f(x)}{x_1-x}=\lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x}
\end{align*}
In Leibniz's notation the passage to the limit in the process of differentiation is symbolically expressed by replacing the symbol $\Delta$ by the symbol $d$, motivating Leibniz's symbol for the derivative defined by the equation
\begin{align*}
\color{blue}{\frac{dy}{dx}=\lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x}}\tag{1}
\end{align*}
Here we have the differences $\Delta x$ and $\Delta y$ which are separate symbols. But in order to obtain the derivative $\frac{dy}{dx}$ we have to assure that $\Delta x$ is not zero and we perform the passage to the limit by means of a transformation which also in the limit avoids division by zero. In this context and with this definition (1) we have to treat $\frac{dy}{dx}$ as single symbol which cannot be separated into two different quantities $dy$ and $dx$. But that's not the end of the story.
- Definition of differentials
The derivative of a function $y=f(x)$ was defined by
\begin{align*}
f^{\prime}(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}=\lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x}
\end{align*}
where $\Delta x=h$. If for a fixed $x$ and a variable $h$, we define a quantity $\varepsilon$ by
\begin{align*}
\varepsilon(h)=\frac{f(x+h)-f(x)}{h}-f^{\prime}(x)=\frac{\Delta y}{\Delta x}-f^{\prime}(x),
\end{align*}
then the fact that $f^{\prime}(x)$ is the derivative of $f$ at the point $x$ amounts to the equation
\begin{align*}
\lim_{h\to 0}\varepsilon(h)=0
\end{align*}
The quantity $\Delta y=f(x+h)-f(x)$ represents the change or increment in the value of the dependent variable $y$ that results when the value $x$ of the independent variable is changed by the amount $\Delta x=h$. Since
\begin{align*}
\Delta y=f^{\prime}(x)\Delta x+\varepsilon \Delta x,
\end{align*}
the quantity $\Delta y$ appears as the sum of two parts, namely, a part $f^{\prime}(x)\Delta x$ which is proportional to $\Delta x$ and a part $\varepsilon \Delta x$ which can be made as small as we please compared to $\Delta x$ by making $\Delta x$ itself small enough. The dominant, linear part in the expression for $\Delta y$ we shall call the differential $dy$ of $y$ and write for it
\begin{align*}
dy=df(x)=f^{\prime}(x)\Delta x\tag{2}
\end{align*}
Here in (2) we can see how $dy$ becomes a symbol by its own. It is by definition and we will shortly see that this kind of definition is in harmony with Leibniz's symbol $\frac{dy}{dx}$.
- For any differentiable function $f$ and for a fixed $x$ this differential (2) is a well-defined linear function of $h=\Delta x$.
For example, for the function $y=x^2$ we have $dy=d(x^2)=2x\Delta x=2xh$.
For the particular function $y=x$ whose derivative has the constant value one, we simply have $dx=\Delta x$. It is then consistent with our definition to write $dx$ for $\Delta x$ when $x$ is the independent variable; hence the differential of any function $y=f(x)$ can also be written as
\begin{align*}
\color{blue}{dy=f^{\prime}(x)dx}.
\end{align*}
- Summary (verbatim from R. Courant): Earlier we used the symbol $dy/dx$ purely symbolically to denote the limit of the quotient $\Delta y/\Delta x$ for $\Delta x$ tending to zero. With our present definition of the differentials $dy$ and $dx$ the derivative $dy/dx$ can actually be considered as the ordinary quotient of $dy$ and $dx$. Here, however, $dy$ and $dx$ are now not in any sense "infinitely small" quantities or "infinitesimals" such an interpretation would be devoid of meaning.
Instead $dy$ and $dx$ are well-defined linear functions of $h=\Delta x$ which for large $\Delta x$ may have large numerical values. There is nothing remarkable in the fact that the quotient $dy/dx$ of those quantities has the same value as the derivative $f^{\prime}(x)$. This is merely a tautology restating the definition of $dy$ as $f^{\prime}(x)dx$.
We will now have a short look at the multi-variable case. We consider for convenience only a bivariate function $u=f(x,y)$. As for functions of one variable we consider
\begin{align*}
\Delta u=f(x+h,h+k)-f(x,y)=h f_x(x,y)+kf_y(x,y)+\varepsilon_1 h+\varepsilon_2 k
\end{align*}
We call the linear part the differential of the function, and write
\begin{align*}
du=df(x,y)=\frac{\partial f}{\partial x}h+\frac{\partial f}{\partial y}k=\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y\tag{3}
\end{align*}
This differential, sometimes called the total differential is a function of four independent variables, namely, the coordinates $x$ and $y$ of the point under consideration and the increments $h$ and $k$ of the independent variables. It simply means, that $du$ approximates to the increment $\Delta u=f(x+h,y+k)-f(x,y)$ of the function, with an error that is an arbitrary small fraction $\varepsilon_1$ of $h$ and $\varepsilon_2$ of $k$, provided that $h$ and $k$ are sufficiently small quantities.
For the independent variables $x$ and $y$ we find from (3) that
\begin{align*}
dx&=\frac{\partial x}{\partial x}\Delta x+\frac{\partial x}{\partial y}\Delta y=\Delta x\\
dy&=\frac{\partial y}{\partial x}\Delta x+\frac{\partial y}{\partial x}\Delta y=\Delta y\\
\end{align*}
Hence, the differential $df(x,y)$ is written more commonly
\begin{align*}
df(x,y)=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy=f_x(x,y)dx+f_y(x,y)dy
\end{align*}
Finally we consider the total differential
\begin{align*}
df=f_xdx+f_ydy
\end{align*}
and the related expression
\begin{align*}
\frac{df}{dy}=f_x\frac{dx}{dy}+f_y\tag{4}
\end{align*}
In (4) we have a function $f=f(x,y)$ and consider $x=x(y)$ as function of $y$, so that $f=f(x(y),y)$ is a function in $y$ and $\frac{dx}{dy}=\frac{d}{dy}x(y)$.