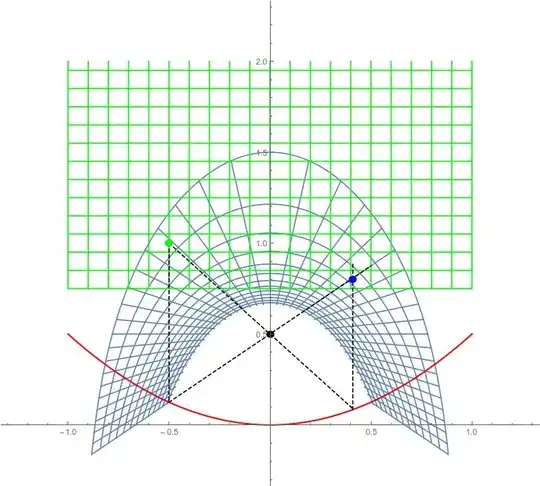
Points reflected by a parabolic mirror create images that appear to be at specific positions on the other side of the mirror. I am attempting to use geometry to find the map from each point in space to the apparent position of their image.
Given the parabolic mirror $y(x) = x^2/(4f)$, my calculations [*] show that a point $\langle x, y\rangle$ on one side of the mirror will be reflected to an image point apparently at
$$\hat x = 2f \left[\frac{y-f}{x} + \sqrt{\left(\frac{y-f}{x}\right)^2 + 1}\right]$$
$$\hat y = f + \left(\frac{x^2/4f - f}{x}\right) \hat{x}$$
For example, the reflection of a grid takes the following apparent shape:
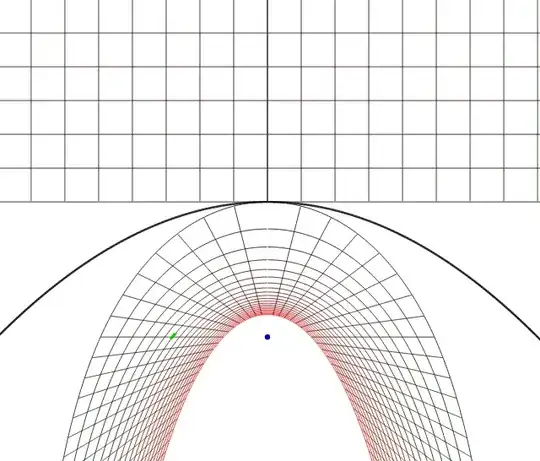
I am attempting to figure out whether the bowed curves created by the horizontal lines form a particular named shape. To do so, I am trying to reparametrize the curve in terms of some $\hat{x}(t)$ and $\hat{y}(t)$, but I'm unsure of how to proceed. For example, I previously suspected that they might be confocal parabolas (though probably not) and would like to rearrange terms so as to show what they are.
[*] My calculations:
I found this formula using the property that a ray of light pointed at the focus will be reflected parallel to the axis of the parabola, and vice versa. Given the point $\langle x,y\rangle$, we drop one vertical (paraxial) line from $\langle x,y\rangle$, which is reflected at the point of intersection with the parabola to a line $\ell_1$ pointing toward the focus. We drop a second line from $\langle x,y\rangle$ itself toward the focus, which is reflected at the point of intersection with the parabola into a vertical (paraxial) line $\ell_2$. The intersection of $\ell_1$ and $\ell_2$ yields the apparent position of the image point $\langle \hat{x}, \hat{y}\rangle$. This method breaks down when $\langle x, y\rangle$ is situated on the axis of the parabola, because then both $\ell_1$ and $\ell_2$ are coincident vertical lines — but I expect this to be a manageable point discontinuity.
The line $\ell_1$ lies between $\langle 0, f\rangle$ and $\langle x, x^2/4f\rangle$. The line $\ell_2$ is a vertical line positioned at wherever the ray from $\langle 0, f\rangle$ toward $\langle x, y\rangle$ intersects the parabola (solvable by quadratic equation).
Note that as a sanity check, the map fixes points on the parabola: if $y = x^2/(4f)$, then $x^2 = 4fy$ and first equation becomes:
\begin{align*} \hat{x} &= \frac{2f}{x}\left[(y-f) + \sqrt{(y-f)^2 + x^2}\right]\\ &= \frac{2f}{x}\left[(y-f) + \sqrt{(y-f)^2 + 4fy}\right]\\ &= \frac{2f}{x}\left[(y-f) + \sqrt{(y+f)^2}\right]\\ &= \frac{2f}{x}\left[2y\right]\\ &= \frac{4fy}{x}\\ &= \frac{x^2}{x}\\ &= x. \end{align*}
Similarly, \begin{align*} \hat y &= f + \left(\frac{x^2/4f - f}{x}\right) \hat{x}\\ &= f + \left(\frac{x^2/4f - f}{x}\right) x\\ &= f + x^2/4f - f\\ &= x^2/4f\\ &= y \end{align*}
New insight — there's a convenient change of coordinates we can make. Instead of rectilinear coordinates $\langle x,y\rangle$, we can use $\langle x, \alpha\rangle$, where $\alpha$ is the angle formed between the point, the focus, and the x-axis. Using one rectilinear coordinate and one focal angle makes sense, because parabolas turn vertical lines into lines angled through the focus and vice-versa, with slope dependent on horizontal position.
We can specify any point in 2D by giving its coordinates $\langle x, \alpha\rangle$. Then the coordinates of the reflected map are simply:
$$\begin{align*}\widehat{x} &= 2f\left[\frac{1+\sin{\alpha}}{\cos{\alpha}}\right]\\\widehat{\alpha}& = \arctan \frac{\frac{1}{4}x^2-f}{x}\end{align*}$$
Wonderfully, $\widehat{x}$ depends only on $\alpha$, and $\widehat{\alpha}$ depends only on $x$.