12

This is a follow-up question to the one with addition instead of multiplication.

Consider $f_1(x)=\sin(x)$ and $f_2(x)=\sin(xf_1(x))$ such that $f_n$ satisfies the relation $$f_n(x)=\sin(xf_{n-1}(x)).$$ To what value does $$L:=\lim_{n\to\infty}\int_0^\pi f_n(x)\,dx$$ converge, where it exists?

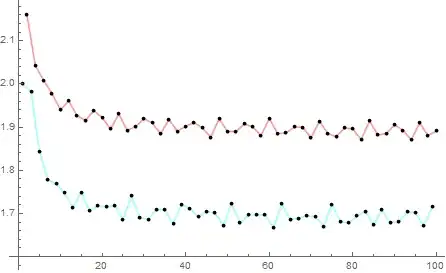
If it does not exist, what are the values of $$L_e:=\lim_{k\to\infty}\int_0^\pi f_{2k}(x)\,dx,\quad L_o:=\lim_{k\to\infty}\int_0^\pi f_{2k-1}(x)\,dx$$ for $k=1,2,\cdots$?

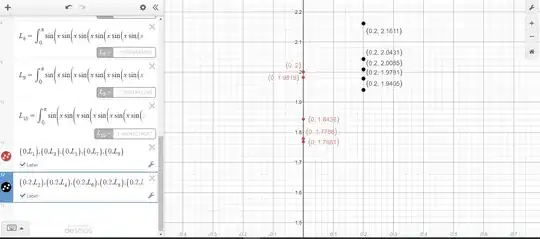
The following diagram shows the values of $L_i$ for even and odd $i$. The odd $i$ all have $x$-coordinate $0.2$ and the even $i$ all have $x$-coordinate $0$.

enter image description here

We can see that if the limits exist, it will be extremely unlikely that they will be the same for even and odd $i$; hence why I asked the final part of the question.

I have tried to use @Tianlalu's method as in my previous question. If we define $t=\text{Sa}(x)$ as the inverse function of $y=t\sin t$ on $[0,\pi]$, then $$t\sin t=x\implies t=\text{Sa}(x)$$ If the limit exists, then $$f_\infty=\sin(xf_\infty)\implies xf_\infty\sin(xf_\infty)=xf_\infty^2\implies f_\infty=\frac{\text{Sa}(xf_\infty^2)}x$$ which is not at all useful since we cannot write $f_\infty$ purely in terms of $x$.

Any ideas on how to continue?

Community
  • 1
ə̷̶̸͇̘̜́̍͗̂̄︣͟
  • 27,005
  • Try a different definition of $\operatorname{Sa}$. – Szeto Oct 07 '18 at 09:40
  • Establishing the inverse function $$\frac{t}{\sin t}=x\implies t=\text{Sa}(x)$$ would have led to a separable term for $f_{\infty}$: $$f_{\infty}(x)=\sin(x f_{\infty}(x))\implies \frac{x f_{\infty}(x)}{\sin(x f_{\infty}(x))}=x \implies x f_{\infty}(x) = \text{Sa}(x) \implies f_{\infty}(x) = \frac{\text{Sa}(x)}{x}$$ However, wouldnt have helped since $\frac{y}{\sin{y}}$ is undefined at $y=0$ and $y=\pi$ – Jameson Oct 08 '18 at 12:12
  • Interestingly, swapping out the sines for cosines would lead to an answer, I believe the integral evaluates to the complex number $$(\ln(2)-1)\pi+i \frac{\pi^2}{2}$$ – Jameson Oct 08 '18 at 12:19
  • @StijnDietz, Integrating a real-valued function cannot yield a complex number which is not in $\mathbb{R}$. The usual notion of integral simply does not allow that. Also, replacing $\sin$ by $\cos$ leads to a similar chaotic behavior that I described in my answer, so it is hopeless to expect the integrals converge. – Sangchul Lee Oct 09 '18 at 01:01
  • I understand your reasoning, but I still obtained that result. I think I have probably ignored a step which renders the solution invalid – Jameson Oct 09 '18 at 09:14

1 Answers1

16

Unlike in the case of iteration $t \mapsto \sin(x+t)$, $f_n(x)$ does not seem converge beyond a certain threshold of $x$. Indeed, plotting the graph of $f_n)$ on $[1,\pi]$ and $201 \leq n \leq 264$ gives

enter image description here

which clearly demonstrates the chaotic behavior as in the logistic map. This can also be glimpsed by the fact that the iteration $t \mapsto \sin(xt)$ resembles that of the logistic map $t \mapsto x t(1-t)$.

Observe that period-doubling cascade occurs within the interval $[0, \pi]$. That is,

  • On the interval of the first bifurcation, $(f_n(x))$ is almost periodic with peroid $2^1 = 2$,
  • On the interval of the second bifurcations, $(f_n(x))$ is almost periodic with peroid $2^2 = 4$,

and so on. The following animation visualizes this situation.

$\hspace{3em}$period-doubling cascade

Thus, unless all the effect of such bifurcations miraculously balance and cancel each other, the values of integrals will oscillate along any subsequences over arithmetic progressions. The graph of $I_k = \int_{0}^{\pi} f_k(x) \, dx $ for $k = 1, \cdots, 100$ seems to support this prediction as well:

$\hspace{5em}$values of integrals

(Even-th terms are joined by red lines, and odd-th terms are joined by blue lines.)

On the other hand, assuming that $x \in [0, \pi]$ and $f_n(x)$ converges, then its limiting value $f_{\infty}(x)$ admits the following expression

$$ f_{\infty}(x) = \begin{cases} \frac{1}{x}\operatorname{sinc}^{-1}\left(\frac{1}{x}\right), & x \geq 1 \\ 0, & x < 1 \end{cases}, $$

where $\operatorname{sinc}^{-1}$ is the inverse of the function $\operatorname{sinc}(x) = \frac{\sin x}{x}$ restricted to $[0, \pi]$. This expression matches the above figure below the threshold.

Sangchul Lee
  • 167,468