A complex approach to integral of cardinal sine

Question

this integral:

$$\int_0^{+\infty}\frac{\sin x}{x}\text{d}x=\frac{\pi}{2}$$

is very famous and had been discussed in the past days in this forum. and I have learned some elegant way to computer it. for example: using the identity: $\int_0^{+\infty}e^{-xy}\sin x\text{d}x=\frac{1}{1+y^2}$ and $\int_0^{\infty}\int_0^{\infty}e^{-xy}\sin x\text{d}y\text{d}x$ and Fubini theorem. the link is here:Post concern with sine integral

In this post, I want to discuss another way to computer it. since$$\int_0^{+\infty}\frac{\sin x}{x}\text{d}x=\frac{1}{2i}\int_{-\infty}^{+\infty}\frac{e^{ix}-1}{x}\text{d}x$$ this fact inspire me to consider the complex integral:$$\int_{\Gamma}\frac{e^{iz}-1}{z}\text{d}z$$
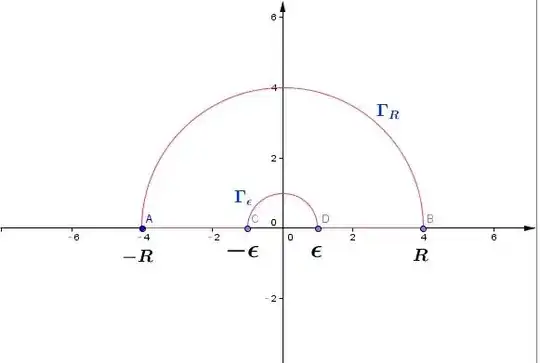
and $\Gamma$ is the red path in the above figure, with counter-clockwise orientation, by Cauchy's theorem, we have $$\int_{\Gamma}\frac{e^{iz}-1}{z}\text{d}z=0$$ the above integral can be written as:$$\int_{-R}^{-\epsilon}\frac{e^{ix}-1}{x}\text{d}x+\int_{\Gamma_{\epsilon}}\frac{e^{iz}-1}{z}\text{d}z+\int_{\epsilon}^{R}\frac{e^{ix}-1}{x}\text{d}x+\int_{\Gamma_{R}}\frac{e^{iz}-1}{z}\text{d}z$$ Let $R\rightarrow +\infty$ and $\epsilon \rightarrow 0$, we have: $$\int_{-R}^{-\epsilon}\frac{e^{ix}-1}{x}\text{d}x+\int_{\epsilon}^{R}\frac{e^{ix}-1}{x}\text{d}x \rightarrow \int_{-\infty}^{+\infty}\frac{e^{ix}-1}{x}\text{d}x=2i\int_0^{+\infty}\frac{\sin x}{x}\text{d}x$$ and $$\int_{\Gamma_{\epsilon}}\frac{e^{iz}-1}{z}\text{d}z=\int_\pi^0\frac{e^{i\epsilon e^{i\theta}}-1}{\epsilon e^{i\theta}}i\epsilon e^{i\theta}\text{d}\theta=i\int_\pi^0(\cos(\epsilon e^{i\theta})+i\sin(\epsilon e^{i\theta})-1)\text{d}\theta \rightarrow 0$$ as $\epsilon \rightarrow 0$
so I am expecting that:$$\int_{\Gamma_{R}}\frac{e^{iz}-1}{z}\text{d}z=-i\pi$$ when $$R \rightarrow +\infty$$ but I can't find it. Could you help me? Thanks very much.

Answer 1

There is the formula $$ \mathrm{pr.v.}\int_{-\infty}^\infty R(x)e^{ix}dx=2\pi i\sum_{y>0}\operatorname{Res} R(z)e^{iz}+\pi i\sum_{y=0}\operatorname{Res} R(z)e^{iz} $$ where the LHS is the principal value, and the RHS is the sum of the residues in the upper half plane, and along the real axis, respectively. This is under the assumption that all poles on the real axis are simple, and $R(\infty)=0$. This is found in Section 5.3, page 158 of Ahlfor's Complex Analysis.

In fact, your question is his first example. Since $\frac{e^{iz}}{z}$ has a single simple pole at $0$ with residue $1$, applying the above formula shows $$ \mathrm{pr.v.}\int_{-\infty}^\infty\frac{e^{ix}}{x}dx=\pi i. $$ Separating into real and imaginary parts, we find $$ \int_{-\infty}^\infty\frac{\sin x}{x}dx=\pi $$ where we drop the principal value since the integral converges. Since $\displaystyle\frac{\sin x}{x}$ is an even function, it follows that $$ \int_0^\infty\frac{\sin x}{x}dx=\frac{\pi}{2}. $$

Answer 2

Way too messy: just take

$$f(z):=\frac{e^{iz}}{z}\;\;,\;\;C_R:=[-R,-\epsilon]\cup \gamma_\epsilon\cup [\epsilon, R]\cup \gamma_R\,\,,\,\,0<\epsilon<<R\,\,,\,\,\epsilon\,,\,R\in\Bbb R\,$$

$$\gamma_h:=\{z\in\Bbb C\;;\;z=he^{it}\,\,,\,0\le t\le \pi\,\,,\,0<h\in\Bbb R\}$$

We use the lemma, and specially its collorary, in the first answer here , to get:

$$\lim_{\epsilon\to 0}\int\limits_{\gamma_\epsilon}f(z)\,dz=\pi i$$

Also

$$\left|\int\limits_{\gamma_R}f(z)\,dz\right|\le \max\frac{e^{-R\sin t}}{R}\pi R\xrightarrow[R\to\infty]{}0$$

so that by Cauchy's Integral Theorem

$$0=\lim_{R\to\infty}\oint f(z)\,dz=\int\limits_{-\infty}^\infty\frac{e^{ix}}{x}dx-\pi i+0\Longrightarrow$$

$$\int\limits_{-\infty}^\infty\frac{\cos x+i\sin x}{x}dx=\pi i$$

Now just compare real and imaginary parts, and take into account that our integrand is an even function...