Let $F: D \rightarrow D$ be a random function on finite domain $D$ of size $n$. It is well-known that, from any $x \in D$, iterating $F$ on $x$ traces out a sequence of values $x, F(x), F(F(x)), \ldots$ that must eventually repeat (since $D$ is finite) and resembles a Greek "$\rho$". The expected number of total elements in this $\rho$ is $\sqrt{n\pi/2}$ with half being on the tail and half on the head. I've seen this stated in several places, but cannot find a proof.
Illustration: In order to clarify what I'm asking (since the comments make it clear that this might be useful), fix an integer $n$. Uniformly sample $a_0 \in [1,n]$ and make a vertex with label $a_0$. Do this again, obtaining a vertex labeled $a_1$ and make a directed edge from $a_0$ to $a_1$ (this does not preclude $a_0 = a_1$). The pigeon-hole principle tells us that eventually we will create a cycle in this digraph; we terminate the process when this occurs. Clearly the graph will look like the letter $\rho$: the "tail" is the part of the graph before we enter the cycle (the tail might have length zero, of course), and the "head" is the is part of the graph comprising the cycle.
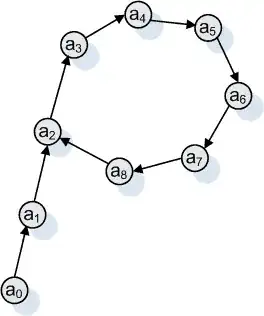
My question is this: what is the expected length of the tail and head, in terms of $n$. Asymptotically, the answer is known to be $\sqrt{n\pi/8}$, but I cannot find a derivation.