2

Based on a random sample (6.3, 1.8, 14.2, 7.6) use the method of maximum likelihood to estimate the maximum likelihoods for $\theta_1$ and $\theta_2$.

$$f_y(y;\theta_1, \theta_2) = \frac{1}{\theta_2- \theta_1} \;, \quad \theta_1 \le \theta_2$$

$$L(\theta_1, \theta_2) = \prod_\limits{i=1}^{n}\frac{1}{\theta_2-\theta_1} \\ = \frac{1}{(\theta_2- \theta_1)^n}\prod_\limits{i=1}^{n}1(\theta_1 \le y_i \le \theta_2) \\ = \frac{1}{(\theta_2- \theta_1)^n}\prod_\limits{i=1}^{n}1(\theta_1 \le y_i)1(y_i \le \theta_2) \\ \text{Let } T = \ln[L(\theta_1, \theta_2)] = -n \ln(\theta_2 - \theta_1) + \sum_\limits{i=1}^n\ln(1(\theta_1 \le \min_i(y_i))1(\max_i(y_i) \le \theta_2)) \\ \begin{cases} -\infty, & \text{if } \theta_1>\min_i(y_i) \text{ or } \theta_2 < \max_i(y_i) \\ -n\ln(\theta_2 - \theta_1), & \text{otherwise} \end{cases} $$

now take the derivative with respect to one of them

$$\frac{\partial{T}}{\partial{\theta_2}} = \frac{-n}{\theta_2 - \theta_1} \\ = \frac{n}{\theta_1 - \theta_2}$$

To maximise this we want the numerator magnitude to be as small as possible, so we set $\theta_2 = \max_i(y_i)$

and for $\theta_1$

$$\frac{\partial{T}}{\partial{\theta_1}}=\frac{n}{\max_i(y_i) - \theta_1}$$

To maximise this, we want $\theta_1 = \min_i(y_i)$

This implies $\theta_1 = 1.8$ and $\theta_2 = 14.2$

If someone could check my correctness particularly around the indicator functions because I'm new to those and anything else you can see wrong in math or formatting.

Actually I think that stuff in yellow directly above is not right. I'm not equating the derivative to 0. I think I got the correct answer regardless. Probably more preferably is to look at the

$$-n\ln(\theta_2 - \theta_1)$$

And know to minimise the value in the brackets will maximise the $\ln[L(\theta_1, \theta_2)]$ function, and coming to the same result that I did illegitimately.

Implies that $\hat{\theta_1} = 1.8$ and $\hat{\theta_2}=14.2$

Michael Hardy
  • 1
Bucephalus
  • 1,386
  • Again, differentiation is not valid here as in your previous questions on MLE with support depending on parameter (hence the indicator functions). – StubbornAtom Oct 05 '18 at 13:51
  • 1
    Given the sample $(y_1,y_2,\ldots,y_n)$, likelihood function of $\theta=(\theta_1,\theta_2)$ is

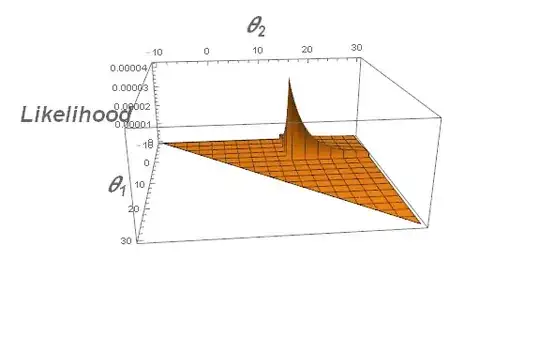
    \begin{align} L(\theta\mid y_1,y_2,\ldots,y_n)&=\frac{1}{(\theta_2-\theta_1)^n}\mathbf1_{\theta_1<y_1,\ldots,y_n<\theta_2} \&=\frac{1}{(\theta_2-\theta_1)^n}\mathbf1_{\theta_1<\min y_i,,,\max y_i<\theta_2} \end{align}

    Clearly, the likelihood function is maximized when $\theta_2-\theta_1$ is minimized.

    Can you now justify why $L(\theta\mid y_1,\ldots,y_n)$ is maximized at $(\theta_1,\theta_2)=\left(\min\limits_{1\le i\le n} y_i,\max\limits_{1\le i\le n} y_i\right)$?

     – StubbornAtom Oct 05 '18 at 13:52
  • A more correct way of saying is that MLE of $(\theta_1,\theta_2)$ is $\left(\min\limits_{1\le i\le n} y_i,\max\limits_{1\le i\le n} y_i\right)$. Rather than MLE of $\theta_1$ is this and MLE of $\theta_2$ is that. It is a maximization problem in two variables $(\theta_1,\theta_2)$. – StubbornAtom Oct 05 '18 at 14:00
  • $\lim_{(\theta_2-\theta_1) \to 0} -n\ln(\theta_2 - \theta_1) = \infty$ @StubbornAtom Thankyou for your guidance. – Bucephalus Oct 05 '18 at 14:07
  • Not sure what you are trying to do with that. Please go through similar MLE questions posted on this site. There are a lot of them. – StubbornAtom Oct 05 '18 at 14:10
  • That was my attempt to answer your justification question. @StubbornAtom I do not I'm not understanding what you're asking If that wasn't what you're looking for. – Bucephalus Oct 05 '18 at 14:14
  • Yet there are highly voted answers here that differentiate to derive the MLE! Like this one. – StubbornAtom Oct 05 '18 at 18:10
  • 2
    Possible duplicate of Stats - Likelihood function – StubbornAtom Oct 05 '18 at 18:16
  • Well see this one @StubbornAtom ? The answer to it? That is the reason I thought I could differentiate in this one too. I didn't just make it up. After you mentioned that and I went back to look for it in the lectures online because I knew I got it from somewhere, now now I have found it: This is where I got the idea of differentiating on these ones: https://math.stackexchange.com/questions/49543/maximum-estimator-method-more-known-as-mle-of-a-uniform-distribution – Bucephalus Oct 05 '18 at 18:17
  • I thought I saw this in an MIT lecture pdf that i downloaded, but now I realise it was a post on here where I saw it, the one I just put in previous comment @StubbornAtom – Bucephalus Oct 05 '18 at 18:19

2 Answers2

5

This is more of an extended comment rather than an answer.

Sometimes a picture will tell you that the maximum likelihood estimates don't occur when derivatives are zero. Here is a plot of the likelihood surface for your data and model:

Likelihood surface

JimB
  • 1,861
  • oh yeah, what program did you do that in @JimB Can you post the code? – Bucephalus Oct 05 '18 at 16:19
  • I read your profile, mathematica for sure. @JimB Is mathematica free? – Bucephalus Oct 05 '18 at 16:20
  • 1
    Mathematica is not free. You can google it to look for a price (as I suppose putting explicit advertisements here is frowned upon). I'll post the code later today when I have time. – JimB Oct 05 '18 at 16:32
  • It's ok, you don't have to. I do not think I would pursue it if it isn't free. Thanks @JimB – Bucephalus Oct 05 '18 at 16:33
  • Such a figure can also be constructed in R which is free (of course, "free" does not include the time it takes to learn it). (And many other "free" software titles will also create such figures.) – JimB Oct 05 '18 at 16:36
  • Yep, i'm learning R. I'm not that advanced yet. I will stick with R for sure. @JimB – Bucephalus Oct 05 '18 at 16:38
  • Sorry @JimB, Michael's answer is more relevant to the question. Cheers. – Bucephalus Oct 05 '18 at 18:26
  • No need to be sorry. My "answer" was just more of a comment to help bring home some of @StubbornAtom 's comments. – JimB Oct 05 '18 at 19:55
1

You have $$ L(\theta_1,\theta_2) = \begin{cases} \dfrac 1 {(\theta_2-\theta_1)^n} & \text{if } \theta_1 \le \min\text{ and } \theta_2\ge\max, \\[6pt] \qquad 0 & \text{otherwise, i.e. if } \theta_1>\min \text{ or } \theta_2 < \max. \end{cases} $$ Since this function gets bigger as the two parameters get closer together, one maximizes it by putting them as close together as the constraints allow. I.e. $\widehat\theta_1= \min$ and $\widehat\theta_2=\max.$

Michael Hardy
  • 1
  • 1
    That's very helpful @MichaelHardy thankyou. I have actually come here to make mistakes and try things that I think I understand, but I don't. I'm also relying on people like you to steer me in the right direction. I had this lecturer once, he was a professor of semi-conductors, etc. I remember him saying once, "Sometimes you think you understand something, and you go on operating with this assumption of understanding, and then ten years later the penny drops, and you go 'aaahhhh, that's how that works'". I remember you have been very helpful to me over the last year. I'm very grateful. Thanks – Bucephalus Oct 05 '18 at 18:05
  • That's good @MichaelHardy but the OP of that one doesn't make it easy to find with a heading like "Stats - Likelihood function" My question has a more specific header stating the operation, the distribution, and that it has two parameters. The alternative question doesn't identify the distribution either in the heading or in the question. I think mine would be easier to find for this problem. – Bucephalus Oct 05 '18 at 18:25
  • @Bucephalus I would have voted to close this as duplicate of the popular post here but the most voted answer is misleading. The post which I have voted for as the original, answers your question sufficiently. No need to fixate over this matter. – StubbornAtom Oct 05 '18 at 18:36
  • @Bucephalus : It said "two-parameter uniform distribution", but I would prefer to see it state explicitly that it means a uniform distribution on the interval $[\theta_1,\theta_2]. \qquad$ – Michael Hardy Oct 05 '18 at 18:38
  • @MichaelHardy changed as requested. – Bucephalus Oct 05 '18 at 18:47