I'm trying to understand a paper that works with tensors. I understand that a tensor of rank 0 is a scalar, a tensor of rank 1 is a vector, and a tensor of rank 2 is a dyad (and therefore it can be considered a matrix, correct me if I'm wrong).
The paper that I am trying to work with is using a rank 3 (i am not sure if it is the rank if someone could explain deeply what's the rank I would be grateful). What I mean by rank three is that has $m*n*z$, that's the image I have about the tensor of rank 3:
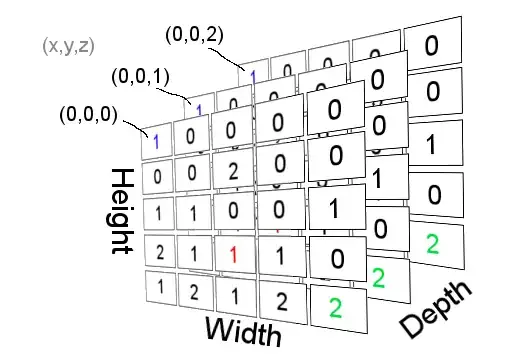
I would like to know if a rank 3 tensor would look like the one in the photo, I imagine it looks like a 3-D matrix, am I right?
Also, if someone could explain how to calculate the rank of a tensor I would pretty much appreciate it.