How does one get the formula for this bijection from $\mathbb{N}\times\mathbb{N}$ onto $\mathbb{N}$?

Question

When showing that $\mathbb{N}\times\mathbb{N}$ is in bijection with $\mathbb{N}$, it seems standard to give a proof by picture that shows a way to systematically weave through all the points in $\mathbb{N}\times\mathbb{N}$ and label each one as you go.

I know there is a polynomial expression for this method, given by $$ J(m,n)=[1+2+\cdots+(m+n)]+m=\frac{1}{2}[(m+n)^2+3m+n] $$ where $m$ is the usual $x$-coordinate and $n$ the usual $y$-coordinate.

But how does one "see" how this formula is arrived at? I know how to manipulate the middle expression to arrive at the rightmost expression, but how does the middle expression relate to the weaving pattern through $\mathbb{N}\times\mathbb{N}$? Thank you.

Answer 1

To weave all the way to $(m,n)$, you first have $m+n$ complete top-left to bottom-right passes, of which the first contains 1 point $(0,0)$, the second two points $(0,1)$ and $(1,0)$, ..., the $m+n$'th $m+n$ points $(0,m+n-1)$ to $(m+n-1,0)$, and then the $m+1$'th point on the next pass is $(m,n)$.

Answer 2

Looking at the diagram, the order is lexicographic, first in $m+n$, then in $m$. The motivation is that it is easy to see you get all the points of $\mathbb{N} \times \mathbb{N}$, so now you just need to figure out what $J(m,n)$ is.

Answer 3

$J(m,n)$ is just the number of points that are before $(m, n)$ in this order. These are the points $(x,y)$ with $x+y < m+n$, and the points $(x,y)$ with $x + y = m + n$ and $x < m$.

The first type of points can be broken down into those with $x+y = 0$ (of which there is $1$), those with $x+y = 1$ (of which there are $2$), and so on up to those with $x +y = m+n-1$, of which there are $m+n$. These are $(m+n-1, 0), (m+n-2, 1), \cdots, (0, m+n-1)$. So there are $1 + 2 + \cdots + (m+n)$ of these.

The second type are just the points $(0,n), (1,n-1), \cdots, (m-1, m+n-1)$. There are $m$ of these.

So the total number of points preceding $(m,n)$ in this order is $$ [1 + 2 + \cdots + (m+n)] + m $$ which is what you wanted.

Answer 4

Say $m$ is the column, $n$ is the row. You want to know how many points you have already counted by the time you get to $(m,n)$, using the picture.

If you go up $n$ rows, you will have counted the first $n$ diagonals in full (since the count starts with $0$). These give you $1+2+3+\cdots+n$ points, since the $n$th downward diagonal has $n$ points in it.

Now, each step you move to the right to get to $(m,n)$ will add another full diagonal that you must have already "added up". This will give you the diagonals with $n+1$, $n+2,\ldots,n+m$ points. This means that, counting only downward diagonals that you have completely counted, you have $$1 + 2 + 3 + \cdots + n + (n+1) + \cdots + (m+n) = \frac{(m+n)(m+n+1)}{2}$$ points.

In addition, you have some points in the diagonal you are on that have been counted. How many? One for each column you moved to the right; there are $m$ of those. So in addition to the points you already added, there are the first $m$ points on the diagonal you are on. So once you get to that point, you have counted $$(1+2+3+\cdots+(n+m) + m = \frac{(m+n)(m+n+1)}{2}+m = \frac{1}{2}\left((m+n)^2+(m+n) + 2m\right)$$ points, which gives the formula.

Answer 5

The formula will manifest itself if you begin by thinking about linear expessions of the form

$\tag 1 z = c + ax + by \quad \text{where } a - b = 1$

observing how they behave on the 45 degree down-slanting lines.

Next you calculate on the $y\text{-axis}$ (view as top/left start of down slash segment),

$\quad J(0,k) = \displaystyle{\frac{1}{2}[k^2 +k]}$

Now the point $J(0,k)$ defines the start of one of our 'down slash' lines; we can write $k = x + y$ and $x = 0$. This allows us to write

$\tag 2 J(0,k) = \displaystyle{\frac{1}{2}[((x+y)^2 +y]}$

Now along the diagonal $x + y = k$ and using $\text{(1)}$ to get the functional coefficient for $a$ when $b =.5$ we know $a = 1.5$. But then by seamless splicing we've found the formula

$\tag 3 J(x,y) = \displaystyle{\frac{1}{2}[((x+y)^2 +3x+ y]}$

Answer 6

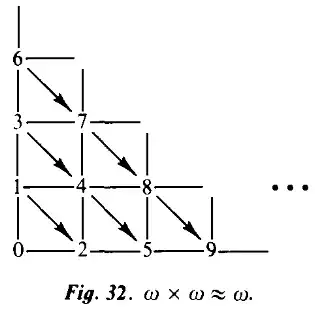
Count the number of elements in each diagonal. The first diagonal contains only the number $0$, the second one contains $1$ and $2$, and so on. In the $kth$ diagonal, there are $k$ elements starting from $k=1$.

After traversing each diagonal, the starting x-coordinate $m$ always resets to $0$ while the starting y-coordinate $n$ increases by $1$ for each diagonal. While traversing each of the diagonals, $m$ increases by $1$ and $n$ decreases by $1$ until $n=0$. The formula $J(m,n)$ is generated as follows:

k-value	first item	second item	third item
$1$	$f(0,0)=0$
$2$	$f(0,1)=1$	$f(1,0)=2$
$3$	$f(0,2)=3$	$f(1,1)=4$	$f(2,0)=5$

To come up with a general expression for the first item in each diagonal, take the sum of all previous $k$ values. For instance, the first element in the diagonal $k=4$ would be $J(0,3)=1+2+3=6$ if the table was to be extended. The first item in each diagonal is generated by adding each of the integers from $1$ to $k-1$, yielding the expression $J(0,k-1)=\frac{(k-1)}{2}(1+(k-1))=\frac{k(k-1)}{2}$. Since each of the elements in the diagonals increases by $1$ each time $m$ increases by $1$, the expression for all items in the diagonals can be generalized as $J(m,n)=\frac{k(k-1)}{2}+m$.

To find $k$ in terms of $m$ and $n$, notice the pattern in each of the diagonals. $m$ increases from $0$ to $k-1$, while $n$ decreases from $k-1$ to $0$. This means $m+n=k-1$, or $k=m+n+1$. Substituting that into the general expression yields $J(m,n)=(m+n+1)(m+n)/2+m=\frac{1}{2} [(m+n)^2+3m+n]$, the desired result.