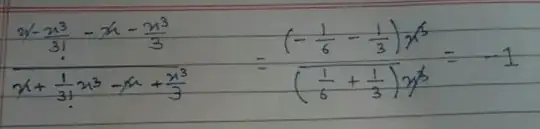Find $\lim\limits_{x\to0}\frac{\sin(x)-\tan(x)}{\arcsin(x)-\arctan(x)}$

Question

Find $\displaystyle \lim_{x\to0}\frac{\sin(x)-\tan(x)}{\arcsin(x)-\arctan(x)}$

I tried using L'hopital's rule but it got very messy very fast

UPDATE- So reading about the Taylor series this is what I have so far

$$\lim_{x\to0}\frac{(x-x^3/3!+x^5/5!-\cdots)-(x+x^3/3+2x^5/5+17x^7/315+\cdots)}{(x+x^2/6+3x^5/40+\cdots)-(x-x^3/3+x^5/5-\cdots)}$$

But I'm still stuck

What else tools have you learned? P.S. $\sin$ seems better than $sin$, and $\to$ is available as \to rather than -> that gives $->$ with redundant spaces between symbols. — xbh, Oct 03 '18 at 04:29
This is the sort of question that lecturers use to torture those students who automatically reach for the Hospital. Use Maclaurin series. — Angina Seng, Oct 03 '18 at 04:38
Some other posts on this site which might help you: Determine $\lim_{x \to 0}{\frac{x-\sin{x}}{x^3}}=\frac{1}{6}$, without L'Hospital or Taylor, Evaluation of $\lim\limits_{x\rightarrow0} \frac{\tan(x)-x}{x^3}$ and Find the limit $\lim_{x\to 0}\frac{\arcsin(x)-\arctan(x)}{x^3}$. — Martin Sleziak, Oct 03 '18 at 04:54
If you just fix then typo in the arcsine series and then do the routine simplifications, you've got the answer. — Michael Hardy, Oct 03 '18 at 05:03
$$ \begin{align} & \frac{(x-x^3/3!+x^5/5!-\cdots)-(x+x^3/3+2x^5/5+17x^7/315+\cdots)}{(x+x^3/6+3x^5/40+\cdots)-(x-x^3/3+x^5/5-\cdots)} \ \ = {} & \frac{(-x^3/3!+x^5/5!-\cdots)-(+x^3/3+2x^5/5+17x^7/315+\cdots)}{(+x^3/6+3x^5/40+\cdots)-(-x^3/3+x^5/5-\cdots)} \ \ = {} & \frac{(-1/3!+x^2/5!-\cdots)-(+1/3+2x^2/5+17x^5/315+\cdots)}{(+1/6+3x^2/40+\cdots)-(-1/3+x^2/5-\cdots)} \to \frac{-1/3! -1/3}{1/6 + 1/3} \end{align} $$ — Michael Hardy, Oct 03 '18 at 05:06

score 4 · Accepted Answer · edited Oct 03 '18 at 07:23

4

You can evaluate this limit using Taylor's expansions. I will write the expansions of the functions below. Note that you can ignore higher powers of x as it is tending to zero. (You will need to think of how many terms to ignore and how many you shouldn't). If you are still not able to evaluate, ask me for help.

\begin{align} \sin x &= x - \frac{x^3}{3!} + \frac{x^5}{5!} + \dotsb \\[4px] \tan x &= x + \frac{x^3}{3} + \dotsb \\[4px] \arcsin x &= x +\frac{1^2}{3!}x^3 + \frac{1^23^2}{5!}x^5 + \dotsb \\[4px] \arctan x &= x - \frac{x^3}{3} + \dotsb \end{align} You can search for more expansions and how to make these expansions in detail on the net or stack exchange itself.

edited Oct 03 '18 at 07:23

egreg

238,574

answered Oct 03 '18 at 04:43

Math Maniac

148

do we just arbitrarily say "oh let's go to the fifth term because it is accurate enough" and then calculate? – John Rawls Oct 03 '18 at 04:47
Evaluating a limit means to bring the given expression from an indeterminate form (here it is 0 divided by 0) to a determinate one. Your aim to evaluate this limit is bringing the expression out of the indeterminate form without changing its value. so when using expansions, you try to use minimum no. Of terms to bring the expression in a determinate one and ignore the rest if they are tending to zero.... – Math Maniac Oct 03 '18 at 04:52
okay for right now i bascially canceled out the x+x^3+x^5... and factored it out and got a fraction with a lot of messy numbers. what do i do in solving this? – John Rawls Oct 03 '18 at 04:54
Try to use only first two terms in expansion in this question... Wait a minute i will send the solution – Math Maniac Oct 03 '18 at 04:55
I edited my ans (posted a photo). Check it out – Math Maniac Oct 03 '18 at 04:58
And yes... Ur expansion for arcsinx is wrong. Instead of x² it should be x³ – Math Maniac Oct 03 '18 at 05:00
If no limit symbol in the front, then you should not write like that. It should be $$ \cdots = \frac {-x^3/2 + o(x^3)} {x^3/2 +o(x^3)} = \frac {-1/2 + o(1)}{1/2 + o(1)} = -1 + o(1) [x \to 0]. $$ – xbh Oct 03 '18 at 05:02

score 3 · Answer 2 · answered Oct 03 '18 at 06:30

This is a nice exercise which shows that a lot more can be achieved using standard limits than what most beginners would think.

We are going to use the following standard limits $$\lim_{x\to 0} \frac{\sin x} {x} =1,\lim_{x\to 0} \frac{1-\cos x} {x^2}=\frac{1}{2},\lim_{x\to 0}\frac{\arctan x} {x} =1$$ All of these are immediate consequences of the first limit.

The numerator of the given expression can be written as $$\frac{\sin x} {x} \cdot x^3\cdot\frac{\cos x-1}{x^2}\cdot\frac{1}{\cos x} $$ and using the standard limit we can replace the above with $-x^3/2$.

The denominator needs a little more effort. Using the identities $$\arcsin x=\arctan\frac{x} {\sqrt{1-x^2}},\arctan x-\arctan y=\arctan\frac{x-y} {1+xy}$$ we can write the denominator as $$\arctan\dfrac{\dfrac{x} {\sqrt{1-x^2}}-x } {1+\dfrac{x^2}{\sqrt{1-x^2}}} $$ and using the limit $\lim_{x\to 0}(\arctan x) /x=1$ the above expression can be replaced by $$\dfrac{\dfrac{x} {\sqrt{1-x^2}}-x } {1+\dfrac{x^2}{\sqrt{1-x^2}}}=\frac{x(1-\sqrt{1-x^2})}{x^2+\sqrt{1-x^2}}$$ Thus the desired limit is equal to the limit of $$\dfrac{-x^3/2}{\dfrac{x(1-\sqrt{1-x^2})}{x^2+\sqrt{1-x^2}}}=-\frac{x^2(x^2+\sqrt{1-x^2})}{2(1-\sqrt{1-x^2})}$$ Multiplying numerator and denominator by $1+\sqrt{1-x^2}$ we can simply the expression above as $$-\frac{(x^2+\sqrt{1-x^2})(1+\sqrt {1-x^2})} {2} $$ and this clearly has limit $-1$ as $x\to 0$.

score 2 · Answer 3 · answered Oct 03 '18 at 05:01

You were on the right track $$A=\frac{\sin(x)-\tan(x)}{\arcsin(x)-\arctan(x)}=\frac{\left(x-\frac{x^3}{6}+\frac{x^5}{120}+O\left(x^7\right)\right)-\left(x+\frac{x^3}{3}+\frac{2 x^5}{15}+O\left(x^7\right) \right)}{\left(x+\frac{x^3}{6}+\frac{3 x^5}{40}+O\left(x^7\right)\right)-\left(x-\frac{x^3}{3}+\frac{x^5}{5}+O\left(x^7\right) \right)}$$ Simplify to get $$A=\frac{-\frac{x^3}{2}-\frac{x^5}{8}+O\left(x^7\right)} {\frac{x^3}{2}-\frac{x^5}{8}+O\left(x^7\right) }=-1-\frac{x^2}{2}+O\left(x^4\right)$$ which shows the limit and how it is approached.

Find $\lim\limits_{x\to0}\frac{\sin(x)-\tan(x)}{\arcsin(x)-\arctan(x)}$

3 Answers3