Help in proving that the given triangle is isosceles

Question

I have the following question with me:

Let $ABCD$ be an isosceles trapezium with $AB$ parallel to $CD$. The inscribed circle of triangle $BCD$ meets $CD$ at $E$. Let $F$ be a point on the internal bisector of angle $DAC$ such that $EF$ is perpendicular to $CD$. Let the circumscribed circle of triangle $ACF$ meet line $CD$ at $C$ and $G$. Prove that triangle $AFG$ is isosceles.

My try:

Define H to be the point of intersection of $CD$ and $AF$. I deduced very few points by simple properties of triangles

$$\frac{AH}{HF} = \frac{AC}{CF} $$ $$\frac{DH}{HC} = \frac{AD}{AC}=\frac{BC}{BD}$$

I also tried ptolemy and angle chasing but couldn't get anything. Any help please.

Answer 1

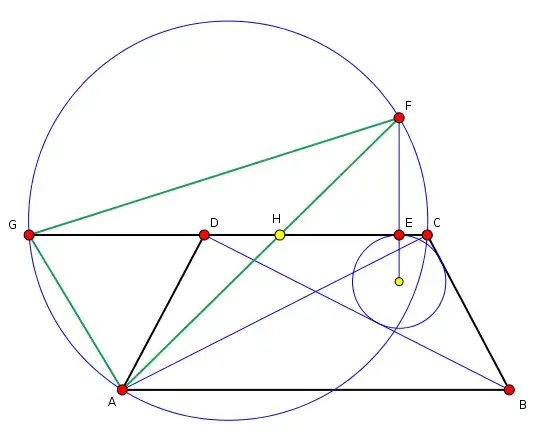
When I'm too lazy to find a suitable chain of established theorems, I tend to resort to algebraic computations. I like using homogeneous coordinates and projective geometry for this. I dislike square roots, as you'd get them when computing the incircle from the circumscribed triangle. So I'll start with that incircle. Without loss of generality, the incircle of $\triangle BCD$ is the unit circle, with $E=[0:1:1]$ at the top to match the figure. Then the other two points of contact can be chosen using the tangent half-angle formulas in such a way that they can represent any point on the unit circle except $E$.

$$E=\begin{bmatrix}0\\1\\1\end{bmatrix}\qquad T=\begin{bmatrix}2t\\t^2-1\\t^2+1\end{bmatrix}\qquad U=\begin{bmatrix}2u\\u^2-1\\u^2+1\end{bmatrix}$$

The tangent line at each of these points can be obtained by multiplying the matrix of the unit circle with the vector. Since that matrix is $\operatorname{diag}(1,1,-1)$ (representing $x^2+y^2-1=0$) you simply negate the last coordinate. Then the points where the tangents intersect can be computed as cross products between the lines.

\begin{align*} B&\sim\begin{bmatrix}2t\\t^2-1\\-t^2-1\end{bmatrix}\times\begin{bmatrix}2u\\u^2-1\\-u^2-1\end{bmatrix}=2(t-u)\begin{bmatrix}t+u\\tu-1\\tu+1\end{bmatrix}\\ C&\sim\begin{bmatrix}2t\\t^2-1\\-t^2-1\end{bmatrix}\times\begin{bmatrix}0\\1\\-1\end{bmatrix}=2\begin{bmatrix}1\\t\\t\end{bmatrix}\\ D&\sim\begin{bmatrix}2u\\u^2-1\\-u^2-1\end{bmatrix}\times\begin{bmatrix}0\\1\\-1\end{bmatrix}=2\begin{bmatrix}1\\u\\u\end{bmatrix} \end{align*}

Assuming $T\neq U$ and therefore $t\neq u$, we can cancel all these coefficients in front of the vectors and continue calculations with the simple representatives. Next we need a reflection in the symmetry axis of the trapezium. You could compute this as the uniquely defined projective transformation which exchanges $C$ with $D$ and exchanges the ideal circle points $I=[1:i:0]$ and $J=[1:-i:0]$ (which is the mark of any orientation-reversing similarity). But I'd rather avoid the complex numbers here, and instead go with the inhomogeneous transformation

$$\begin{pmatrix}P_x\\P_y\end{pmatrix}\mapsto \begin{pmatrix}C_x+D_x-P_x\\P_y\end{pmatrix}= \begin{pmatrix}\frac1t+\frac1u-P_x\\P_y\end{pmatrix}$$

Written in homogeneous coordinates and avoiding divisions by multiplying everything with $tu$ this becomes $P\mapsto RP$ with the reflection matrix

$$R=\begin{bmatrix}-tu&0&t+u\\0&tu&0\\0&0&tu\end{bmatrix}$$

We can use this to find $A$ as

$$A=RB=\begin{bmatrix}t+u\\tu(tu-1)\\tu(tu+1)\end{bmatrix}$$

To compute the angular bisector through $A$ would again entail a square root, but we can also define that same line as the line through $A$ and the reflection of the origin $O=[0:0:1]$ (which is the center of the incircle).

$$l_{AF}\sim A\times(RO)=tu\begin{bmatrix}tu(tu-1)\\tu(t+u)\\(t+u)(1-tu)\end{bmatrix}$$

This line we intersect with $[1:0:0]$, the vector for the line $1x+0y+0=0$, to obtain $F$.

$$F\sim\begin{bmatrix}tu(tu-1)\\tu(t+u)\\(t+u)(1-tu)\end{bmatrix}\times\begin{bmatrix}1\\0\\0\end{bmatrix}=-(t+u)\begin{bmatrix}0\\tu-1\\tu\end{bmatrix}$$

Omitting this factor $t+u$ here assumes $t\neq-u$ or in other words $T,U$ are not mirror images with respect to the vertical axis through the unit circle. If they were, then $A$ and $B$ would be the same point, so I think this is again a fair assumption.

Now we need the circle through $A,C,F$, which can be computed as the conic through $A,C,F,I,J$ with $I=[1:i:0]$ and $J=[1:-i:0]$ as the ideal circle points. First define two degenerate conics through $A,C,I,J$, each given as the symmetric product of a pair of (complex) lines. Then the circle is the linear combination which also passes through $F$.

$$ Q_1=(I\times A)\odot(J\times C)=\tfrac12\bigl((I\times A)(J\times C)^T+(J\times C)(I\times A)^T\bigr) \\ Q_2=(J\times A)\odot(I\times C)=\tfrac12\bigl((J\times A)(I\times C)^T+(I\times C)(J\times A)^T\bigr) \\ Q\sim(F^TQ_2F)Q_1-(F^TQ_1F)Q_2=i u t^3 (u^2 + 1)\cdot\\ \begin{bmatrix} 2 u t^2 (tu + 1) & 0 & -t^2 (u^2 + 1) \\ 0 & 2 u t^2 (tu + 1) & -t (2t^2u^2 + u^2 - 1) \\ -t^2 (u^2 + 1) & -t (2t^2u^2 + u^2 - 1) & 2 u (tu - 1) (t^2 + 1) \end{bmatrix}$$

I have to concede that this circle is quite a beast. We have non-degeneracy conditions $t\neq 0$ and $u\neq 0$, since either of these would lead to one tangent being parallel to $CD$ and this to points at infinity. The point $G$ can be computed as

$$G\sim (D^TQD)C - 2(C^TQD)D=2(t-u)^2 \begin{bmatrix}t-u\\tu(tu+1)\\tu(tu+1)\end{bmatrix}$$

Now we need to express the isosceles condition. One possibility: $F$ lies on the orthogonal bisector of $AG$. To describe that bisector you can join the midpoint $M$ between $A$ and $G$ to the point $N$ at infinity orthogonal to $AG$.

$$M\sim G_3A+A_3G=2t^2u(tu+1)\begin{bmatrix}1\\tu^2\\u(tu+1)\end{bmatrix}\\ N\sim\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix}(A\times G)= -2tu^2(tu+1)\begin{bmatrix}t\\1\\0\end{bmatrix}$$

Now three points are collinear if their determinant is zero.

$$\det(F,M,N)=\begin{vmatrix} 0 & 1 & t \\ tu-1 & tu^2 & 1 \\ tu & u(tu+1) & 0 \end{vmatrix} = 0$$

So $F$ does indeed lie on the perpendicular bisector, as claimed. Q.e.d.

Answer 2

Starting with the posted figure, extend $AD$ to $K$, join $FK$, $FC$, draw $FD$ through to $M$, join $GK$, $GM$, extend $FE$ to $L$ on the incircle, and through $L$ draw a line parallel to $CG$.

Then granting, as seems to be the case, that $L$ lies on circle $ACF$, and that $M$ lies on the parallel through $L$, it would follow that$$\triangle FGM\sim\triangle FEC$$because$$\angle GFM=\angle EFC$$since they stand on equal arcs $GM$ and $CL$, and$$\angle FMG=\angle FCE$$ since they stand on common arc $GF$. Therefore $\angle MGF=\angle CEF$ is right and $FM$ is a diameter of circle $ACF$.

And since $D$ lies on this diameter, it follows that$$DK=DC$$and$$DG=DA$$whence by SAS$$\triangle GDK\cong\triangle ADC$$

And finally, since$$\angle KGF=\angle FGC=\angle KAF=\angle FAC$$making$$KF=FC$$then by AAS$$\triangle KGF\cong\triangle CAF$$whence$$GF=AF$$and triangle $GFA$ is isosceles.

I am unable to prove that $L$ lies on circle $ACF$, and that $M$ lies on the parallel through $L$, but of several figures and attempts, each missing a link somewhere, this is the nearest I get to a purely geometric understanding of this interesting phenomenon.