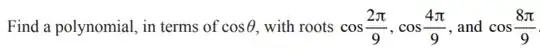The question gives a hint; first, 'find the general solution for $cos$ $5θ = cos$ $4θ$'
So far my progress with this hint is;
$ 5θ = 2πk + 4θ $ or $ 5θ = 2πn - 4θ $
$ θ = 2πk$ or $ 9θ = 2πn $ , where $n , k $ are integers
I'm stumped after this and have to idea how to attack the question. Any hints would be appreciated
From what you've got and using the hint, we see that $\cos\frac{2\pi}{9},\cos\frac{4\pi}{9},\cos\frac{8\pi}{9}$ satisfy $$\cos(5\theta)=\cos(4\theta),$$ i.e. $$\cos(2\theta+3\theta)=2\cos^2(2\theta)-1,$$ i.e. $$\cos(2\theta)\cos(3\theta)-\sin(2\theta)\sin(3\theta)=2(2c^2-1)^2-1$$ where $c:=\cos\theta$.
$$(2c^2-1)(4c^3-3c)-2sc(3s-4s^3)=2(2c^2-1)^2-1$$ where $s:=\sin\theta$.
$$(2c^2-1)(4c^3-3c)-2c(3s^2-4s^4)=2(2c^2-1)^2-1,$$ i.e. $$(2c^2-1)(4c^3-3c)-2c(3(1-c^2)-4(1-c^2)^2)=2(2c^2-1)^2-1,$$ i.e. $$16 c^5 - 8 c^4 - 20 c^3 + 8 c^2 + 5 c - 1=0$$ Since $c=1=\cos(2n\pi)$ and $c=-\frac 12=\cos(\frac{6\pi}{9})$ are the solutions, we get $$(2 c + 1) (c - 1) (8 c^3 - 6 c + 1)=0$$
It follows that the answer is$$8\cos^3\theta - 6\cos\theta + 1=0$$
(Note that we have only five distinct values in $\cos(2k\pi),\cos(\frac{2n\pi}{9})$.)
$$\cos\frac{2\pi}{9}+\cos\frac{4\pi}{9}+\cos\frac{8\pi}{9}=2\cos\frac{3\pi}{9}\cos\frac{\pi}{9}+\cos\frac{8\pi}{9}=\cos\frac{\pi}{9}+\cos\frac{8\pi}{9}=0;$$ $$\cos\frac{2\pi}{9}\cos\frac{4\pi}{9}+\cos\frac{2\pi}{9}\cos\frac{8\pi}{9}+\cos\frac{4\pi}{9}\cos\frac{8\pi}{9}=$$ $$=\frac{1}{2}\left(\cos\frac{2\pi}{3}+\cos\frac{2\pi}{9}+\cos\frac{2\pi}{3}+\cos\frac{8\pi}{9}+\cos\frac{4\pi}{9}+\cos\frac{2\pi}{3}\right)=\frac{1}{2}\cdot\left(-\frac{3}{2}\right)=-\frac{3}{4}$$ and $$\cos\frac{2\pi}{9}\cos\frac{4\pi}{9}\cos\frac{8\pi}{9}=\frac{8\sin\frac{2\pi}{9}\cos\frac{2\pi}{9}\cos\frac{4\pi}{9}\cos\frac{8\pi}{9}}{8\sin\frac{2\pi}{9}}=\frac{\sin\frac{16\pi}{9}}{8\sin\frac{2\pi}{9}}=-\frac{1}{8}.$$ Id est, we got the following polynomial. $$x^3-\frac{3}{4}x+\frac{1}{8}.$$ For $x=\cos\theta$ we obtain: $$\cos^3\theta-\frac{3}{4}\cos\theta+\frac{1}{8}.$$
If $9t=2n\pi,t=\dfrac{2n\pi}9$ where $n=0,\pm1,\pm2,\pm3,\pm4$
$$\implies\sin5t=\sin(2n\pi-4t)=-\sin4t\ \ \ \ (1)$$
Using Prosthaphaeresis Formulas
$$\sin5t-\sin t=2\sin2t\cos3t=4\sin t\cos t\cos3t$$
By $(1),$ $$\sin t(4\cos t\cos3t+1)=-4\sin t\cos t\cos2t$$
If $\sin\ne t=0,n\ne0$
$$4\cos t\cos3t+1=-4\cos t\cos2t$$
$$\iff4\cos t(4\cos^3t-3\cos t)+1=-4\cos t(2\cos^2t-1)$$ which is a bi-quadratic equation on rearrangement whose roots are $\cos\dfrac{2n\pi}9$ where $n=1,2,3,4$
As for $n=3,\cos\dfrac{2n\pi}9=\dfrac12,$ divide the bi-quadratic equation by $(2\cos t-1)$
