Help understanding solution in volume of Solid of Revolution $y=12-x^3$ and $y=12-4x$ revolved around 1.) x-axis 2.) y-axis

Question

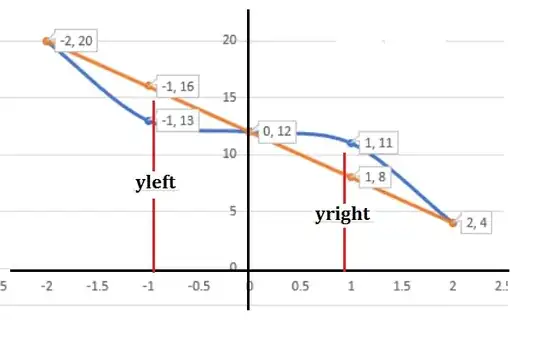
The curves look like this. The solution for the volume used a circular disk for the x axis of revolution. I got the total volume from doubling the volume by rotating the solid formed from $x=0$ to $x=2$. Trying to apply the same concept from the boundary $x=-2$ to $x=0$, I get a different answer.

Solution: Boundary: $x=0$ to $x=2$

$$\frac V2=\pi\int_{0}^2[(12-x^3)^2-(12-4x)^2] dx$$

V=~449

Boundary: $x=-2$ to $x=0$

$$\frac V2=\pi\int_{-2}^0[(12-4x)^2-(12-x^3)^2] dx$$

$V=~756$

What am I missing?

For y-axis for same reason the two half volumes would not be the same. — Narasimham, Sep 27 '18 at 20:44

Narasimham · Answer 1 · 2018-09-28T04:43:15.913

1

By Pappu's thm rotated Volume equals section Area $* 2 \pi \cdot y_{CG} $ where CG is center of gravity.

The section areas are same. But since on the left $y_{CG}$ is greater so is its volume is greater. (756>449)

Total volume is the sum of the two:

$$V_1+V_2 =\pi\int_{-2}^2[(12-x^3)^2-(12-4x)^2] dx=1205$$

edited Sep 28 '18 at 04:43

answered Sep 27 '18 at 20:35

Narasimham

40,495

If the volumes aren't equal then rotating one side and multiplying by 2 is wrong then? Should I rotate the whole figure and add the 2 volumes? So it'll be 449+756=1205 – Renzo Sep 28 '18 at 03:14
Yes.as given above – Narasimham Sep 28 '18 at 04:47

Help understanding solution in volume of Solid of Revolution $y=12-x^3$ and $y=12-4x$ revolved around 1.) x-axis 2.) y-axis

1 Answers1