1

Given a line segment of $1$ unit in length construct a line segment that is

  • $\sqrt{13}$ in length
  • $\sqrt{22}$ in length

Is it best to use the root spiral of theodorus or is there a more efficient method? Thanks in advance.

Community
  • 1
Matlab rookie
  • 75
  • Note that $\sqrt {13}$ is the hypotenuse of the right triangle with legs $2,3$. Now, $22$ isn't the sum of two squares so that's a bit harder, but this question should help. – lulu Sep 26 '18 at 13:31

2 Answers2

5

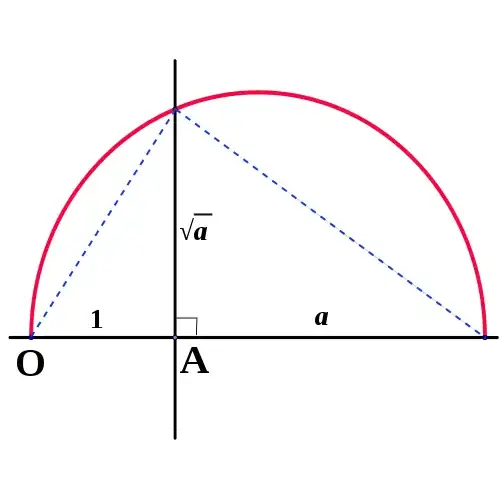
It is easy to construct $\sqrt a$ for each $a$ that is constructible: enter image description here

(picture from commons.wikimedia)

lhf
  • 216,483
5

In order to construct a line segment with length $\sqrt{13}$, I would construct it as the hypotenuse of a right triangle such that the length of the other two sides are $2$ and $3$. After that, I would construct another right triangle whose catheti have lengths $\sqrt{13}$ and $3$. The length of its hypotenuse will then be equal to $\sqrt{22}$.

José Carlos Santos
  • 427,504