1

I’m stuck proofing the difference formula $\sin (\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta$.

Given this diagram:

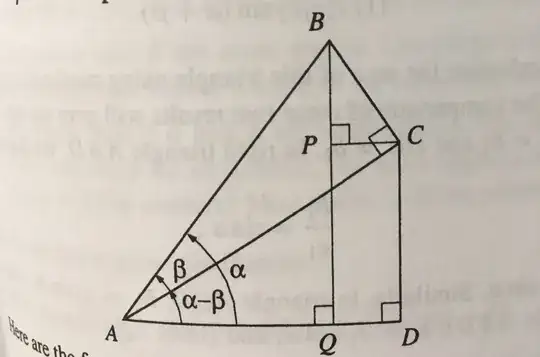
enter image description here

$$\sin (\alpha - \beta) = CD/AC = PQ/AC = (BQ-BP)/AC=BQ/AC-BP/AC$$

Now we need to relate that back to sine and cosine of alpha and beta:

$$BQ/AC = ???$$

I’m stuck here because $\sin \alpha = BQ/AB$ and $\cos \beta = AC/AB$. Multiplying those fractions together won’t give me $BQ/AC$.

I thought I had the right idea, but I’m stuck. Hints are appreciated.

bjcolby15
  • 3,599
BMBM
  • 2,461
  • $$BQ = AB\sin\alpha$$ $$AC = AB\cos\beta$$ $$\frac{BQ}{AC} = \frac{AB\sin\alpha}{AB\cos\beta} = \frac{\sin\alpha}{\cos\beta}$$ – Larry Sep 25 '18 at 02:14
  • @Larry So $BP/AC$ can then be expressed also the same way? I find that confusing since then we have $AC=\cos \beta$ in both fractions as denominator? – BMBM Sep 25 '18 at 05:26
  • Actually, I try to express BP/AC in the same way and prove your question, but it doesn't seem quite easy to do that. – Larry Sep 25 '18 at 10:40

1 Answers1

2

Let's instead prove the sum formula: $\sin(\alpha)=\sin(\alpha-\beta)\cos(\beta) + \sin(\beta)\cos(\alpha-\beta)$.

To do this, explain why the first summand on the right equals $CD/AB$, while the second summand on the right equals $BP/AB$ (hint: use similar triangles!). Combining these two gives you the sum formula.

To get the difference formula, draw the same diagram but with $\beta$ going clockwise.

Danny Stoll
  • 401
  • 1
    So as far as I can see the angle at $PBC$ is equal to $\alpha - \beta$. But i can’t seem to use that in my proof without making a circular argument. – BMBM Sep 25 '18 at 05:22
  • Can you give me a hint for the similar triangles argument? I can’t see it. – BMBM Sep 26 '18 at 00:31
  • Notice that angle APC equals angle CAD, so their complements, namely angle BCP and angle ACD, are also equal. Thus triangle BPC is similar to triangle ADC. This implies that $AD/AC=BP/BC$, so $$\sin(\beta)\cos(\alpha-\beta) = (BC/AB)(AD/AC) = (BC/AB)(BP/BC) = BP/AB$$ as desired. – Danny Stoll Sep 28 '18 at 19:14
  • Thank you! I understand now, although I think in your first sentence: "Notice that angle $APC$ equals angle $CAD$, ..." I guess you mean "Notice that angle $ACP$ equals angle $CAD$, ..." . Because I can't see any angle $APC$? – BMBM Sep 29 '18 at 00:01
  • 1
    Whoops! Yes, it should read $ACP$. – Danny Stoll Sep 29 '18 at 02:20