18

$\mathbf {ijk}=-1$ is part of the famously stone-carved formula by Sir William Rowan Hamilton, allowing the multiplication of triplets. There is already an intuition question on the topic of quaternions, and a beautifully illustrated post on 3D stereographic projections of quaternion rotations in 4D in the 3Blue1Brown youtube channel.

The question is very specific about how to picture in a geometric or intuitive way the equality $\mathbf {ijk}=-1$ part in the formula

$$\mathbf {i}^2 = \mathbf {j}^2 = \mathbf {k}^2 =\mathbf {ijk}=-1 $$

Attempt: $\mathbf i$, $\mathbf j$ and $\mathbf k$ act on the left of a quaternion as a pure rotation; hence,

$$\mathbf {ijk}\overset{?}=\mathbf {(ij)k}$$

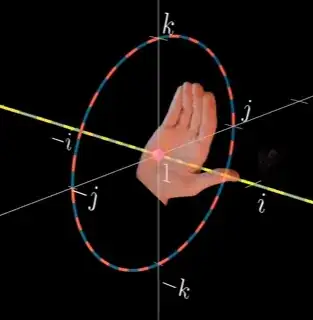
and $\mathbf {i}$ acts on $\mathbf {j},$ rotating $\mathbf {j}$ into $\mathbf {k}$ in keeping with 3Brown1Blue's Grant Sanderson's "right-hand rule", illustrated with the 3D diagram below, corresponding to the stereographic projection of a 4D hypersphere of quaternions with norm $1$ and $0$ real component, where the $-\infty,$ $-\mathbf i,$ $1,$ $\mathbf i,$ $+\infty$ yellow line is the projection of a circle in 4D running through $-1,$ and centered at $0,$ passing through $-\mathbf i$ and $+\mathbf i;$ while the red-blue $\mathbf j,$ $\mathbf k,$ $-\mathbf j,$ $-\mathbf k$ circle corresponds to the 3D projection of a sphere in the 4D hypersphere passing through $-1,$ and centered at $0,$ and reaching both $\pm \mathbf k$ and $\pm \mathbf j.$ Rotating in the direction of $\mathbf i$ (i.e. multiplying on the left by $\mathbf i$) would amount to sliding the yellow line in the direction of the thumb, while rotating the red-blue circle following the clenching of the rest of the fingers:

enter image description here

and resulting in

$$\begin{align}\mathbf {ijk}&\overset{?}=\mathbf {(ij)k}\\ &=\mathbf {kk}\\ &=\mathbf k^2 =-1 \end{align}$$

Antoni Parellada
  • 8,889
  • 6
    As with all questions that ask for help with building intuition, I am reminded of a quote of John von Neumann: "in mathematics you don't understand things, you just get used to them". – Aweygan Sep 25 '18 at 01:25
  • 5
    We should always try to understand the things we work with. But in the meantime, not understanding something shouldn't get in the way of working with it. – Misha Lavrov Sep 27 '18 at 20:35

5 Answers5

10

You are right this can be viewed as a composition of (4D) rotations and, in fact, this particular example provides an example of a very interesting phenomenon in 4D Euclidean geometry. Namely, if we start with an arbitrary point $q$ in $\mathbb{H}$,

$$q = a + bi + cj + dk$$

then

$$kq = ak + bki + ckj + dkk$$

(the scalars commute so this is okay) which becomes through the usual formulas,

$$\begin{align} kq &= ak + bj - ci - d\\ &= -d - ci + bj + ak\end{align}$$

This is a rotation in 4D space as can be seen by noting that its matrix form is

$$k \equiv \mathbf{K} := \begin{bmatrix} 0 && 0 && 0 && -1 \\ 0 && 0 && -1 && 0 \\ 0 && 1 && 0 && 0 \\ 1 && 0 && 0 && 0 \end{bmatrix}$$

which is easily seen to be orthogonal, i.e. $\mathbf{K}^T \mathbf{K} = \mathbf{I}$. Moreover, the expansion by cofactors and minors (which is very easy) shows $\mathrm{det}(\mathbf{K}) = 1$, so it is indeed a proper rotation (i.e. is not a rotoreflection).

Knowing that it's a rotation, the natural question is: what is it a rotation about? In 4D, we don't rotate around axes that are lines, but rather we rotate around planes, because a line gives "too much freedom" for a single angle of rotation to capture in the same way that we don't "rotate around a point" in 3D with a single angle of rotation. (This may be hard to visualized, but that's 4D for 'ya.)

So which plane is it? We may be tempted to note that while this permutes all 4 coordinates, you might see that it fixes the plane where $a = -d$ and $b = -c$, i.e. the quaternions of the form

$$a + bi - bj - ak$$

are unchanged under the transformation $\mathbf{K}$. Now you might think that a bit strange, given that is not a simple coordinate plane - and it is, indeed, an omen. In fact, if you see something like this happening in maths, chances are something very strange is going on - it's no guarantee, but your spidey sense should tingle at it and you should feel disturbed. In particular, we can decompose this a bit further. Taking another look we can see that it is actually the composition of two rotations: one of which does

$$(a + bi + cj + dk) \mapsto (-d + bi + cj + ak)$$

which fixes the $ij$-plane, and is a 90-degree, followed by

$$(a + bi + cj + dk) \mapsto (a - ci + bj + dk)$$

which fixes the $1k$-plane. This is also a 90-degree rotation. These two planes are orthogonal, and when you have a rotation in 4D space that is formed by the composition of two rotations of the same angle through two orthogonal planes, you get what is called an isoclinic or Clifford rotation that in fact fixes infinitely many planes, one other of which we just found. This is a very strange phenomenon with no simple analogue in 3D: in 3D a rotation will fix only one line, its axis, unless it's a degenerate rotation by zero degrees.

Likewise, the rotations by action of $j$ and $i$ are similar Clifford rotations, and they all together act to bring $1$ to $-1$ via $-1 = i(j(k(1))) = ijk$. If you want, you can think of this approximately as being like a hyperdimensional version of a Rubik's cube where you twist the sides through several different positions to move one colored patch from one side to another (not exactly, though, since here the whole "cube" is rotating, but an approximate analogy - the gist is the chained transformations.).

Tiago André
  • 318
The_Sympathizer
  • 19,651
  • 2
    Really cool! Thank you. – Antoni Parellada Sep 25 '18 at 02:34
  • 3
    @Antoni Parellada : Thanks. I do believe that in many cases there really is an intuition to be had (even if you can't necessarily visualize it in a way that does it full justice, but relate it to at least in-principle more understandable concepts like rotations), and not that you should just "Get used to it" :) – The_Sympathizer Sep 25 '18 at 02:40
9

A mental image is arguably asking slightly too much. For instance, if you gave someone a verbal or written description of a dodecahedron, would that suffice as a means to help them mentally picture it? Maybe for some, but not for me (or maybe I just don't like dodecaherons like I do the other Platonic solids).

But a satisfying visual-kinesthetic explanation is possible using the idea of spin.

Rotating a solid object $360$ degrees, its initial orientation matches its final orientation. However, if the orientation is entangled with its environment, its "entangled orientation" is different. One can imagine a belt, or multiple belts, attached to a spinning cube for example:

$\hskip 2in$ cubespin

It turns out, it requires $720^{\circ}$ of "spinning" before "entangled orientation" reverts back to its initial state, and this can be seen with the so-called plate trick: put a plate on your hand (palm up), hold it out, then rotate it $360^{\circ}$ (under your arm) - it will not be back to normal - and then another $360^{\circ}$.

(One can make all this mathematically rigorous by invoking homotopy.)

In the so-called spin group $\mathrm{Spin}(3)$, this means if $S_{360}$ is the spin by $360^{\circ}$, it is not equivalent to the identity rotation $S_0$, however $(S_{360})^2=S_{720}$ is equal to $S_0$. Algebraically, the latter is equivalent to saying $S_{360}$ is its own inverse, i.e. $(S_{360})^{-1}=S_{360}$, and this can be depicted with the string trick:

$\hskip 2in$ inverse

The above shows that a twisting the ball once around one direction is equivalent to twisting the ball once around the other way. One can also depict it with the belt trick:

$\hskip 2in$ belt

This one shows two full rotations is equivalent to no rotation, but with the belt attached (to an invisible object, say) at a different place relative to the axis of rotation.

The belt trick can also be used to demonstrate $\mathbf{ijk}=-1$, but first we have to figure out how to interpret quaternions as rotations. (The whole reason they were discovered/invented in the first place was to generalize the use of complex numbers describing 2D rotations to 3D.) Unit quaternions have polar forms $p=e^{\theta\mathbf{v}}$ for unit vectors $\mathbf{v}$ (i.e. square roots of negative one, so Euler's formula applies), and the effect of conjugating a 3D vector $\mathbf{x}$ by $p$ (yielding $p\mathbf{x}p^{-1}$) is rotating $\mathbf{x}$ around the oriented axis $\mathbf{v}$ by the angle $2\theta$.

Since $\mathbf{v}$ has polar form $\exp(\frac{\pi}{2}\mathbf{v})$, the corresponding rotation is $180$ degrees around $\mathbf{v}$ (in either direction). So, take a belt and hold it straight out in front of you (like nunchuks I guess?). Pay attention to the orientation of the belt buckle, as you (in order) rotate it around the $\mathbf{k}$-, $\mathbf{j}$- and $\mathbf{i}$-axes. The effect is the buckle itself will be back to its original position, but the belt will have a $360^{\circ}$ twist in it, represented by the quaternion $-1$.

anon
  • 151,657
  • Can you please explain "unit quaternions have polar forms $p=e^{\theta\mathbf{v}}$ for unit vectors $\mathbf v$"? – Antoni Parellada Sep 27 '18 at 23:33
  • @AntoniParellada Sure. Quaternions are formal sums of scalars and 3D vectors. If you look at the (quaternion) multiplication table of $\bf i$, $\bf j$, $\bf k$ you'll notice the scalar parts are minus the dot product and the vector part is the cross product. Thus, ${\bf uv}=-{\bf u}\cdot{\bf v}+{\bf u}\times{\bf v}$. You can use this to show the sqrts of $-1$ are precisely the unit vectors. Thus, $e^{\theta\bf u}=\cos(\theta)+\sin(\theta){\bf u}$. Every quaternion has a polar form $re^{\theta \bf u}$ for some magnitude $r$ and unit vector $\bf u$. – anon Sep 27 '18 at 23:52
  • Try to find the polar form of $1+{\bf i}+{\bf j}+{\bf k}$ as an exercise, if your want. – anon Sep 27 '18 at 23:53
  • Some terminology clarifications... in ${\bf uv}=-{\bf u}\cdot{\bf v}+{\bf u}\times{\bf v}$ in your comment above, both $\bf u$ and $\bf v$ are quaternions of the form $(0,\bf u)$ and $(0,\bf v),$ i.e. quaternions with only vector components, correct? (The representation of quaternions as $(0,\bf u)$ explained here). – Antoni Parellada Sep 29 '18 at 15:16
  • As for the equation $e^{\theta\bf u}=\cos(\theta)+\sin(\theta){\bf u},$ I see a very frugal explanation here, which would imply that $u$ and $v$ are "unit imaginary quaternions". What would be the form of these unit imaginary quaternions? Would they have zero scalar component and either $1\bf i,$ $1\bf k,$ or $1\bf j$? That is to say, only one of the imaginary components present and of magnitude 1? – Antoni Parellada Sep 29 '18 at 15:16
  • Well, ask and you shall be given, it turns out that the answer to the question is given here by you - unit imaginary quaternions are $(0,a\bf i+b\bf j+c\bf k)$, such that $a^2 + b^2 + c^2 =1,$ because $(a\bf i+b\bf j+c\bf k)^2=-1.$ – Antoni Parellada Sep 29 '18 at 15:44
  • And, comment to self, the $2\theta$ rotation has an explanation here. – Antoni Parellada Sep 29 '18 at 16:01
  • The formula for $\bf uv$ implies unit vectors $\bf u$ are sqrts of $-1$, and so $e^{\theta\bf u}=\cos(\theta)+\sin(\theta)\bf u$ follows by the same logic as Euler's formula for $e^{i\theta}$ (power series stuff). The formula for $\bf uv$ also implies that if ${{\bf u},{\bf v},{\bf w}}$ is an oriented orthonormal basis then it has the same multiplication table as ${{\bf i},{\bf j},{\bf k}}$. Define $p=e^{\theta\bf u}$ and $L_p(x)=px$ and $R_p(x)=xp$. Then $L_p$ and $R_p$ each are rotations by $\theta$ in the $1\bf u$ and $\bf vw$-planes, but different directions in the $\bf vw$ plane. – anon Sep 29 '18 at 18:41
  • Indeed, they're rotations in the $1\bf u$-plane by the same reasons multiplying by $e^{i\theta}$ is a rotation by $\theta$ in $\Bbb C$. As for $L_p$ in the $\bf vw$-plane, one can write $a{\bf v}+b{\bf w}=(a+b{\bf u}){\bf v}$, and for $R_p$ one can use ${\bf v}p=\overline{p}{\bf v}$ since ${\bf v}$ is perpendicular to $p$'s vector part. Inverting $L_p$ or $R_p$ changes the direction of rotation in the two planes, so the effect of $L_p\circ R_p^{-1}$ is cancelling the angles in the $1\bf u$-plane and doubling in the $\bf vw$-plane. – anon Sep 29 '18 at 18:44
  • If one restricts such a function $pxp^{-1}$ to vectors $\bf x$, it is thus a 3D rotation around $\bf u$ by the angle $2\theta$. Also thanks for the bounty! – anon Sep 29 '18 at 18:45
  • Can you sketch a drawing? – Antoni Parellada Sep 30 '18 at 23:45
  • It'd take some time and effort to draw that carefully. Maybe someone can record me doing it tomorrow. But it'd be easiest if you just do the process correctly. Rotate $180^{\circ}$ around the the three axes in the correct order. You need to do $z$-axis, then $y$-axis, then $x$-axis, and make sure your axes are oriented according to the right-hand rule. If you do them out of order, you will wind up with something equivalent to $0^{\circ}$ (which $720^{\circ}$ is) because ${\bf kji}=+1$. – anon Sep 30 '18 at 23:54
  • 1
    Okay I had to take a picture with my nose a couple times but here's four pictures. You can also do a different illustration of ijk=-1 with your hand, see here. I will update my answer with more details from these comments sometime later this week. – anon Oct 01 '18 at 00:37
  • 1
    I can't rotate that imaginary plate under my arm two full rotations. At least not without dislocating a shoulder and a few other joints :-) – Jyrki Lahtonen Oct 02 '18 at 03:33
  • 1
    @JyrkiLahtonen If it helps, do the second rotation over your head. :) – anon Oct 02 '18 at 04:41
3

In one of Cohl Furey's videos on octonions, she posted a very intuitive way to think about quaternions (I've linked to the appropriate segment). This gives intuition about why say, $ij = k$, and then $ijk = k^2 = -1$ follows easily.

Here's the gist:

enter image description here

If you multiply two consecutive quantities (in a clockwise direction), you get the next value. If you move counterclockwise (i.e., against the arrows) then the same rule works but you get a minus sign. So $jk = i$ and $ik = -j$, for example.

I'm not sure if this is original to Cohl, but I first saw this in her lecture. This also might not qualify as intuition as asked for in the body of your post, but it should qualify as a mental image like you asked for in your title.

JavaMan
  • 13,153
  • Could you summarize the argument for the benefit of people who can't watch a video right away? –  Sep 25 '18 at 04:03
  • @Rahul: Done. Sorry I couldn't do it earlier as I was using my mobile phone. – JavaMan Sep 25 '18 at 12:37
3

THIS IS NOT AN ANSWER - Just an appendix / extended comment that doesn't belong to the original post...

@anon's answer contains a "belt trick" to illustrate the $\bf{ijk}=-1.$ Explained in words was rather confusing, but (after his pictures holding his belt included in the comments to his post as a link, I believe the idea can be illustrated as follows:

enter image description here

Here is the part of @anon's answer relevant to the illustration:

Since $\mathbf{v}$ has polar form $\exp(\frac{\pi}{2}\mathbf{v})$, the corresponding rotation is $180$ degrees around $\mathbf{v}$ (in either direction). So, take a belt and hold it straight out in front of you (like nunchuks I guess?). Pay attention to the orientation of the belt buckle, as you (in order) rotate it around the $\mathbf{k}$-, $\mathbf{j}$- and $\mathbf{i}$-axes. The effect is the buckle itself will be back to its original position, but the belt will have a $360^{\circ}$ twist in it, represented by the quaternion $-1$.

Background elements:

Unit imaginary quaternions are of the form

$$\left( 0, a{\bf i} + b{\bf j} + c {\bf k } \right)$$

such that $a^2 + b^2 + c^2 = 1.$

It is proven here that

$$\left( a{\bf i }+ b{\bf j} + c {\bf k} \right)^2=-1$$

allowing their expression as

$$e^{\theta \vec {\bf v}}= \cos \theta + \sin \theta\; \vec {\bf v}$$

A rotation of $180$ degrees around the unit imaginary vector $\vec {\bf v}$ will correspond to

$$e^{\frac \theta 2 \vec {\bf v}}=e^{\frac\pi 2 \vec {\bf v}}$$

Here's a link.

Antoni Parellada
  • 8,889
1

$\mathbf{ijk}=-1$ doesn't need to be true. If you choose $\mathbf{ijk}=1$ instead, you get an isomorphic algebra.

$\mathbf i, \mathbf j, \mathbf k$ represent 180° rotations around the $x,y,z$ axes. The rotations negate two of the coordinates and leave the third unchanged. The three rotations taken together negate each coordinate twice, so they have no effect in total. So $\mathbf{ijk}$ must be $1$ or $-1$, and it turns out that either choice works.

The choice is not entirely meaningless since it does pin down the meaning of the $\mathbf i, \mathbf j, \mathbf k$ symbols. $\mathbf i^2 = \mathbf j^2 = \mathbf k^2 = \pm 1$ tells you that they must be rotations by multiples of 180°. $\mathbf i^2 = \mathbf j^2 = \mathbf k^2 = -1$ tells you that it must be an odd multiple of 180°; you can see this through the Dirac belt trick or related illustrations that have been mentioned in other answers. But that tells you nothing about how the three axes are oriented relative to each other. $\mathbf{ijk} = \pm1$ tells you that they're orthogonal, and the choice of $1$ or $-1$ fixes the handedness of the coordinates.

benrg
  • 310