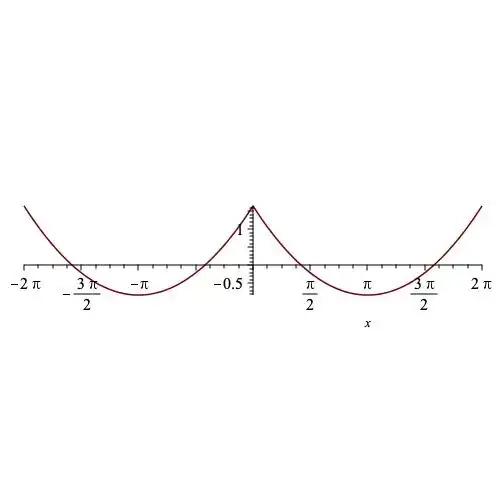
Given $$f(x) = \sum_{n=1}^\infty \frac{\cos(nx)}{n^2}$$
By plotting graph, it seems to be that this function is not differentiable at $x=0$, two sided limits are not equal with each other but I cannot show how. Also it seems that $f'(x)$ is not uniformly convergent however I cannot see how I can use that.