1

I am trying to play around applying transformations to rectangle.

In this picture, I skewed a box by -30 degrees on the Y axis to get the following. The purple box is the transformed box and the dashed border, transparent box is the original one.

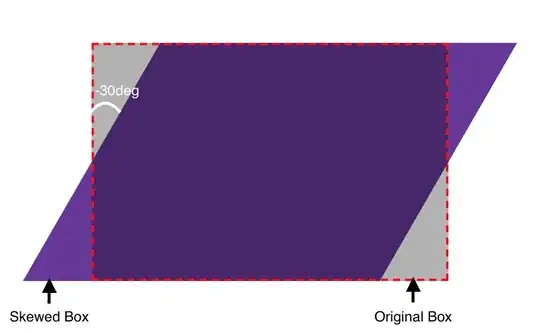
enter image description here

I was thinking if I can achieve the same by first skewing on the X axis and then rotating the box to compensate for the skewing done.

enter image description here

But I got a very different result. enter image description here

At first, it's probably because or the order of those transformations done so I flipped them but this time I got another different result. Essentially the opposite of the previous one.

enter image description here

What I am unable to understand is that from Picture 2, it seemed like skewX and rotate by the same amount would work but it didn't.

Can someone please explain why?

Praveen Puglia
  • 111
  • 1
    In the first skew the length of the shorter sides stayed the same. And rotation didn't change that. In the other skew on the other hand you tilted that shorter side, but the height of the box stayed constant. To compensate that shorter side had to become longer. – Jyrki Lahtonen Sep 17 '18 at 19:23
  • For one relation between skews, rotations and scalings, see this oldie. You can get another explanation to your observation by using the transformation matrices much like what was done there. Are you familiar with matrices? – Jyrki Lahtonen Sep 17 '18 at 19:25
  • I am familiar with matrices. Didn't think of that before posting! – Praveen Puglia Sep 17 '18 at 19:32
  • Great! In that case I can post an answer using matrices. – Jyrki Lahtonen Sep 17 '18 at 19:35
  • At first I didn't see that you tried both orders in the combined transformation. I added the other direction to my answer as well. – Jyrki Lahtonen Sep 17 '18 at 20:04

2 Answers2

3

Skewing on the $y$-axis preserves the lengths of the shorter, vertical sides of the rectangle; the horizontal sides become longer.

Skewing on the $x$-axis preserves the lengths of the longer, horizontal sides of the rectangle; the vertical sides become longer.

So the resulting parallelograms will have the same vertex angles $60^\circ, 120^\circ, 60^\circ, 120^\circ$ but different ratios of the sides. Skewing on the $y$-axis produces a long and thin shape (the two side lengths get further apart), while skewing on the $x$-axis produces a short and wide shape, relatively speaking (the two side lengths get closer together).

Numerically, if the rectangle started out with sides $a$ and $b$, one of the methods will produce a parallelogram with sides $a$ and $\frac{b}{\cos 30^\circ}$, while the other will produce a parallelogram with sides $\frac{a}{\cos 30^\circ}$ and $b$.

Misha Lavrov
  • 142,276
2

A skew by angle $\theta$ in the direction of the $y$-axis (=your first skew) is a linear transformation with the matrix $$ S_y=\left(\begin{array}{cc}1&0\\ \tan\theta&1\end{array}\right). $$ (This is assuming that the origin is a fixed point. If not, then you get an affine transformation instead, but that won't change the following argument in any essential way.)

Similarly, a skew in the direction of the $x$-axis is given by the matrix $$ S_x=\left(\begin{array}{cc}1&\tan\theta\\ 0&1\end{array}\right). $$

For its part, rotation by $\theta$ is represented by the matrix $$ R=\left(\begin{array}{cc}\cos\theta&-\sin\theta\\ \sin\theta&\cos\theta\end{array}\right). $$

The combined transformation of an $x$-skew followed by a rotation is thus given by the matrix product $$ RS_x=\left(\begin{array}{cc}\cos\theta&\sin\theta-\sin\theta\\ \sin\theta&\sin^2/\cos\theta+\cos\theta\end{array}\right)=\left(\begin{array}{cc}\cos\theta&0\\ \sin\theta&1/\cos\theta\end{array}\right), $$ where I used the trig identities $\tan\theta=\sin\theta/\cos\theta$ and $\sin^2\theta+\cos^2\theta=1$ to simplify the matrix.

You see that this matrix product is different from the one representing the $y$-skew, and that's what you are seeing.

Do observe the second column of the matrix of the combined transformation. Its top entry is equal to zero. This means that the combined transformation does map the $y$-axes to itself. But you see from the bottom entry of that second column that the combination stretches the distance between points on the $y$-axis by a factor of $1/\cos\theta.$ This factor is $>1$ when $\theta$ is non-trivial.

The difference between $1$ and $1/\cos\theta$ shows in your images in that the left vertical side of the purple parallelogram in the last image is longer thatn the height of the rectangle.

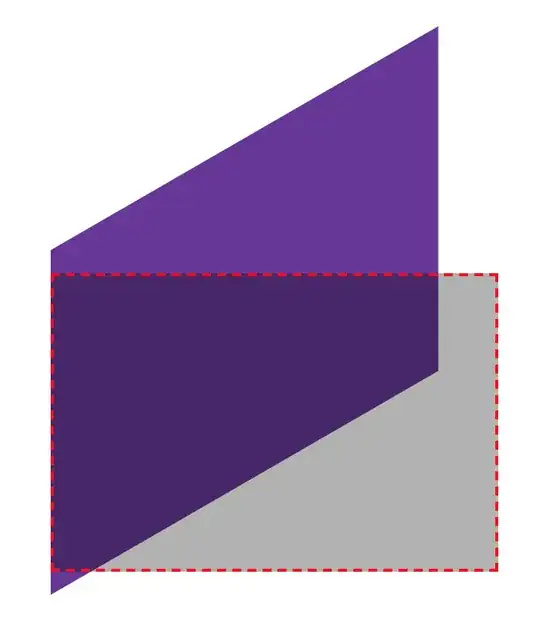
On the other hand, if you first rotate and the $x$-skew, you get the matrix product $$ S_xR=\left(\begin{array}{cc}1/\cos\theta&0\\ \sin\theta&\cos\theta\end{array}\right). $$ Again, the $y$-axis is mapped onto itself, but this time the stretching factor is $\cos\theta <1$. You see this in your third image.

It may be worth pointing out that the determinants of all these matrices are equal to one. This reflects the fact that the total area of the figure stays the same in all skews and rotations even though individual sides of a rectangle will stretch or shrink as case may be.

Jyrki Lahtonen
  • 133,153