2

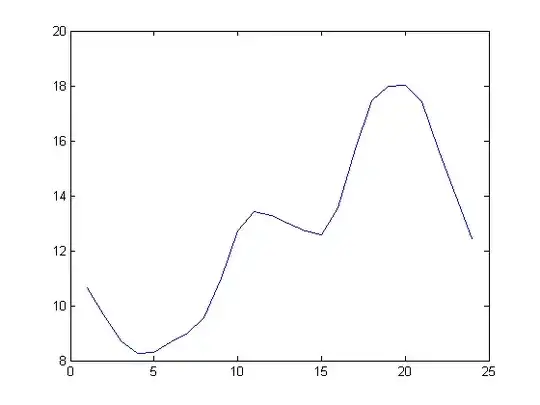
I have 24 values for $Y$ and corresponding 24 values for $t$. The Y values are measured experimentally, while t has values $t=1,2,\dots 24$.

I want to find the relationship between Y and t as an equation using Fourier analysis.

I wrote the following MATLAB code:

Y=[10.6534
    9.6646
    8.7137
    8.2863
    8.2863
    8.7137
    9.0000
    9.5726
   11.0000
   12.7137
   13.4274
   13.2863
   13.0000
   12.7137
   12.5726
   13.5726
   15.7137
   17.4274
   18.0000
   18.0000
   17.4274
   15.7137
   14.0297
   12.4345];

ts=1; % step    
t=1:ts:24; % the period is 24 
f=[-length(t)/2:length(t)/2-1]/(length(t)*ts); % computing frequency interval    
M=abs(fftshift(fft(Y)));    
figure;plot(f,M,'LineWidth',1.5);
grid % plot of harmonic components    
figure; plot(t,Y,'LineWidth',1.5);
grid % plot of original data Y    
figure; bar(f,M); grid % plot of harmonic components as bar shape

the results of the bar figure was and now is:

t vs. Y

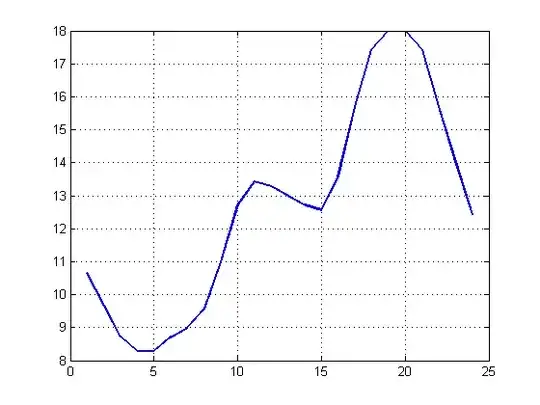
Now, I want to find the equation for these harmonic components which represent the data. After that I want to draw the original data Y with the data found from the fitting function and the two curves should be close to each other.

Should I use cos or sin or -sin or -cos? In other words, what is the rule to represent these harmonics as a function: $Y = f ( t )$ ?

Emre
  • 2,783
  • Depends a bit on the algorithm used by Matlab. Can you not read off the code to see what they use? I don't have Matlab, so I can't check. – Raskolnikov Mar 26 '11 at 22:38
  • It is not a matter of Matlab program, it is a concept problem. How to get a function of known data Y=f(t) using fourier analysis. From reading some books and papers, the plot of points is analysed by fourier series, then, from its harmonic components, an equation could be written and built in some approach which is I am trying to find. –  Mar 26 '11 at 23:31
  • What do the harmonic components represent? Amplitudes? Then what are the phases? If you don't know that, you can't retrieve the function. – Raskolnikov Mar 26 '11 at 23:52

1 Answers1

2

You can dispatch this problem with one line of MATLAB, f=fit(t',Y,'fourier8'), the result of which is:

f = 

 General model Fourier8:
 f(x) = 
           a0 + a1*cos(x*w) + b1*sin(x*w) + 
           a2*cos(2*x*w) + b2*sin(2*x*w) + a3*cos(3*x*w) + b3*sin(3*x*w) + 
           a4*cos(4*x*w) + b4*sin(4*x*w) + a5*cos(5*x*w) + b5*sin(5*x*w) + 
           a6*cos(6*x*w) + b6*sin(6*x*w) + a7*cos(7*x*w) + b7*sin(7*x*w) + 
           a8*cos(8*x*w) + b8*sin(8*x*w)
 Coefficients (with 95% confidence bounds):
   a0 =       4.889  (-4.318, 14.09)
   a1 =      -13.85  (-26.55, -1.152)
   b1 =       6.884  (-5.952, 19.72)
   a2 =      -2.135  (-2.839, -1.431)
   b2 =          13  (-2.486, 28.48)
   a3 =       6.205  (-2.355, 14.76)
   b3 =        8.53  (0.1128, 16.95)
   a4 =       6.537  (-2.725, 15.8)
   b4 =       3.137  (2.424, 3.851)
   a5 =       5.048  (0.8798, 9.216)
   b5 =      -1.603  (-6.124, 2.918)
   a6 =        1.68  (1.289, 2.071)
   b6 =      -2.345  (-5.843, 1.153)
   a7 =      -0.158  (-1.539, 1.223)
   b7 =      -1.358  (-2.395, -0.3211)
   a8 =     -0.5341  (-1.093, 0.02453)
   b8 =     -0.3162  (-0.6587, 0.02635)
   w =      0.1994  (0.19, 0.2087)

plot(t,f(t) looks like this: Eight-term Fourier series approximation

The answer to your question then is: you usually use both sine and cosine terms. The exception is if the signal is odd or even, in which case you use just sines and cosines, respectively.

Emre
  • 2,783