Where is this trig equation derived from?

Question

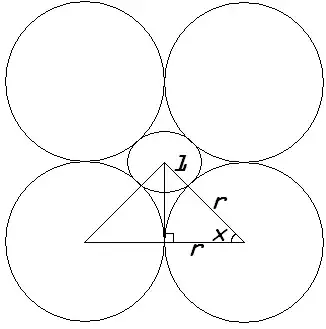
In the first, top rated, comment on the original post linked below, the author wrote the function $r = \dfrac {\cos(x)} {1−\cos(x)}$. I do not understand how they got to this equation. I get how they solved for $x$ in their first step. Can you please explain how they solved for $r$.

This is the picture of the problem, where we are solving for $r$, given $x = \dfrac {n-2}{2n}$

Original Post Numbers of circles around a circle

You have linked to a user profile, not a comment or answer. Hence I honestly have no idea what this question is about... — Xander Henderson, Sep 11 '18 at 22:06

Deepesh Meena · Accepted Answer · 2018-09-15T00:16:58.970

3

In the right Triangle, we can write $\cos x $ as Base divided by the hypotenuse

$$\cos x=\frac{r}{r+1}$$

$$\frac{1}{\cos x}=1+\frac{1}{r}$$

$$\frac{1}{r}=\frac{1}{\cos x}-1$$ $$\frac{1}{r}=\frac{1-\cos x}{\cos x}$$ $$r=\frac{\cos x}{1-\cos x }$$

edited Sep 15 '18 at 00:16

answered Sep 11 '18 at 18:37

Deepesh Meena

4,408

Where is the 1 from in the denominator at the beginning? Shouldn't it be r/r+L – Levi Kline Sep 11 '18 at 18:41
1

it is the length of the hypotenuse in the right triangle which is $r+1$ – Deepesh Meena Sep 11 '18 at 18:42
1

it is 1 it is not L – Deepesh Meena Sep 11 '18 at 18:42
1

you misreading 1 as L here it is 1 – Deepesh Meena Sep 11 '18 at 18:43
If my center circle radius is 100, then is it r/r+100? – Levi Kline Sep 11 '18 at 18:43
yes you are correct if the raduis of the center circle is 100 – Deepesh Meena Sep 11 '18 at 18:47
I figured out that with a radius of 100, I had to make the equation r=100(cosx/1-cosx) – Levi Kline Sep 12 '18 at 03:28
can I ask you how you went from your third line of math to your fourth (second to last)? How did you transfer that -1 the way you did? – Levi Kline Sep 12 '18 at 04:19
@LeviKline $\frac{1}{r} = \frac{1}{\cos x} - 1 = \frac{1}{\cos x} - \frac{\cos x}{\cos x} = \frac{1 - \cos x}{\cos x}$. – N. F. Taussig Sep 12 '18 at 09:40
@N.F.Taussig I see, thank you. I should have thought about multiplying for a common denominator. Silly me! Thank you for the clarification. – Levi Kline Sep 12 '18 at 13:38

Where is this trig equation derived from?

1 Answers1