Let $n$ be a positive integer, and for $i = 1, 2, \ldots, n$, let $x_i$ be the $i^\text{th}$ abscissa for $n$-point Gaussian quadrature, and $w_i$ the associated weight, so that $-1 < x_1 < x_2 < \cdots < x_n < 1$, $x_{n-i+1} = -x_i$, $w_{n-i+1} = w_i > 0$, and $\sum_{i=1}^n w_i = 2$.
It is natural to wonder if the right-hand side of the numerical integration formula: \begin{equation*} \int_{-1}^1 f(x)\,dx \bumpeq \sum_{i=1}^n w_if(x_i) \end{equation*} (this is exact when $f$ is a polynomial of degree less than $2n$) is a Riemann sum.
That is, if we define $s_i = \sum_{k=1}^i w_k - 1$ ($i = 0, 1, \ldots, n$), so that $w_i = s_i - s_{i-1}$ ($i = 1, 2, \ldots, n$), and $-1 = s_0 < s_1 < s_2 < \cdots < s_{n-1} < s_n = 1$, and $s_{n-i} = -s_i$ ($i = 0, 1, \ldots, n$), do we have $x_i \in [s_{i-1}, s_i]$ ($i = 1, 2, \ldots, n$)?
Indeed, we do. As is shown here,
$$
s_0 < x_1 < s_1 < x_2 < s_2 < \cdots < s_{n-1} < x_n < s_n.
$$
An illustration, for $n = 1$ to $9$:
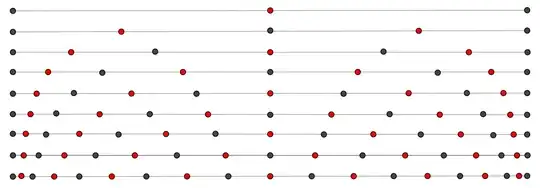
The picture becomes clearer if we work in terms of $y_i = (2/\pi)\sin^{-1}(x_i)$ and $t_i = (2/\pi)\sin^{-1}(s_i)$.
We have $y_{n-i+1} = -y_i$ ($i =
1, 2, \ldots, n$), $t_{n-i} = -t_i$ ($i = 0, 1, \ldots, n$), and:
$$
-1 = t_0 < y_1 < t_1 < y_2 < t_2 < \cdots < t_{n-1} < y_n < t_n = 1.
$$
A pattern is visible when one displays the subintervals
$[t_{i-1}, t_i]$ with the interior points $y_i$ aligned vertically.
For $n = 64$:
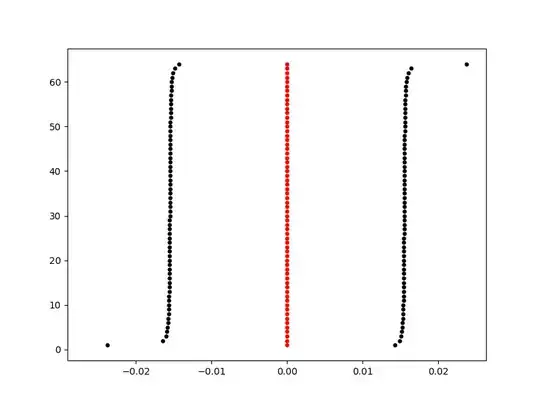
If we define $u_i = y_i - t_{i-1} = t_{n-i+1} - y_{n-i+1}$ ($i = 1, 2, \ldots, n$), then $\sum_i u_i = (t_n - t_0)/2 = 1$, and the following approximation seems surprisingly accurate: $$ u_i \bumpeq \frac{1}{2n + 1}\left( 2 + \frac{1}{n\tan(\pi\eta)}\tan\left( \frac{\pi}{2}\left( 1 - \frac{2i - 2\eta - 1}{n} \right)\right)\right), $$ where the 'optimum' value of $\eta$ depends on $n$, but seems to consist of a constant term of about $0.348$ plus a small positive term of order about $n^{-2}$. Like the $u_i$ themselves, the approximate values sum exactly to $1$, thanks to this identity: $$ \tan\theta = \frac{1}{n}\sum_{i=1}^n\tan\left(\frac{\pi}{2} - \frac{(2i-1)\pi}{2n} + \frac{\theta}{n}\right) \quad \left(n \geqslant 1, \ \theta \ne k\pi + \frac{\pi}{2}\right). $$ (Proof: see here or here.)
Leaving aside the problem of explaining the closeness of this approximation, the question I am asking here is whether, for all $n$ (the value of $n$ is absent from the notation I am using, but we could instead use a notation like $u_i^{(n)}$), we have: $$ u_1 > u_2 > \cdots > u_n. $$ Equivalently, $\sin^{-1}(x_i) - \sin^{-1}(s_{i-1}) > \sin^{-1}(x_{i+1}) - \sin^{-1}(s_i)$, i.e.: $$ x_i\sqrt{1 - s_{i-1}^2} - s_{i-1}\sqrt{1 - x_i^2} > x_{i+1}\sqrt{1 - s_i^2} - s_i\sqrt{1 - x_{i+1}^2} \quad (1 \leqslant i < n). $$