I am quite stuck on how to differentiate log(y) with respect to y. When I googled it, I seen many websites state that d(log(y))/dy is 1/yln(10). However, the question I have attached requires me to differentiate xylog(y) w/ respect to y, but I got a different answer to my teacher. I have attached the question, teacher’s answer & my answer. Thanks 
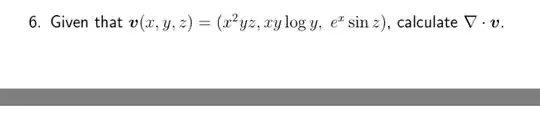
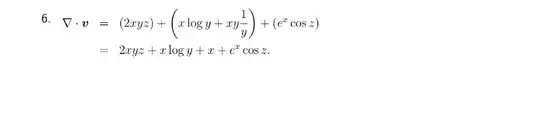
Asked
Active
Viewed 3,376 times
0
user564900
- 37
- 2
- 7
1 Answers
1
You are interpreting the question as using base $10$ while your teacher uses base $e$ for the logarithm.
Hence the difference in your solution.
Your answer is correct if base $10$ is indeed used in the logarithm though the popular default is base $e$ in calculus. Not always, but popular.
Edit:
$$\frac{\partial}{\partial y}(xy \log_b y)=x \log_b y+\frac{xy}{\ln b}$$
You are treating the question as $b=10$ while your teacher is treating $b=e$.
Siong Thye Goh
- 149,520
- 20
- 88
- 149
-
Thank you for your reply. When I changed the base to e, I got an answer of (x+xln(y))/ln(10), which is still different to my teacher’s answer and im not sure why. – user564900 Sep 11 '18 at 01:31
-
Your teacher is computing $\frac{\partial}{\partial y} (xy \ln y)$. – Siong Thye Goh Sep 11 '18 at 01:33
-
So did he make a mistake? – user564900 Sep 11 '18 at 01:36
-
when a typical maths person write $\log$, he means $\log_e$. You two are answering different questions. – Siong Thye Goh Sep 11 '18 at 01:37
-
I thought log is assumed to be log base 10 and ln is log base e – user564900 Sep 11 '18 at 01:39
-
yup, that is how most are taught at secondary school. but as you go higher, most people use base $e$. – Siong Thye Goh Sep 11 '18 at 01:42
-
Ah this is so annoying. People should stick to the right convention. Thank you for clearing this up for me though, much appreciated – user564900 Sep 11 '18 at 01:43
-
For your interest, a discussion link on the choice. – Siong Thye Goh Sep 11 '18 at 01:53