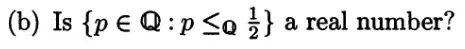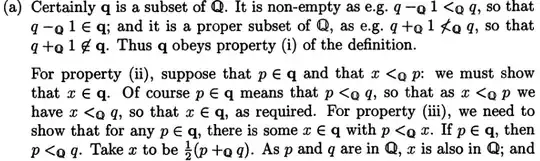The problem is: How do we define/construct the real numbers?
We can define/construct the rational numbers by iteratively adding, subtracting the number one and dividing the quantities we get. But that won't give us the irrationals.
Now we can't just say "the irrationals are everything else" because that is not a definition.
So if we can't define the irrationals why do we need them? Well, because in comparing sizes of the rationals we can "get as close as we like" between them. This implies that we desperately want there to be a "continuum" that if we go between two numbers we can pass through every value between.
The rationals fail this. And we can't just declare something exists without knowing what it is. So is there any way we define this continuum using the concept of rational numbers?
Well, the rational numbers get close and for every desired value in this continuum we can get an infinite number of rational numbers that get close to it with infinite precision by considering this infinite set of rational numbers.
In other words. For every value in the continuum, there is a unique set of all the rational numbers that are less than it that we can uniquely associate with this value.
And that is the answer to our problem. We will define/construct the real numbers by these unique sets of rational numbers by associating each real number with a unique set of rational numbers. (and vice versa.)
Now, you might quibble, but those sets are associated with the real numbers. The are not the real numbers themselves. Point taken. But I claim it does not matter; it is a one to one association and thus a unique defining. As these are abstractions an association (provided it always exists and is always unique and consistant) is all there is.
Hence: A real number is defined by the unique set of all rational numbers that are less than it.
These sets are called Dedekind left sets and as they are uniquely associated we define a "real number" as being the set.
==== old answer below ====
The book is replacing everything you know about numbers with something different.
The problem is if we use the concept of numbers that we grew up with, CONTWGUW, then we can define the rationals but we can not define the reals. We can't just say the reals are "everything else" or with the "holes filled in".
So the book is doing something radical. It is defining a mathematical system that is not CONTWGUW but absolutely equivalent to it and it is going to use that instead. Forever and always. It will never use CONTWGUW again.
We start by defining the rationals as we always have and the arithmetic from this. But because we are going to abandon it entirely we want to indicate it is the old arithmetic, we will note it with the $_\mathbb Q$ symbol.
For example $q +_\mathbb Q 1$ will mean $q$ plus $1$ with the old arithmetic. And $q <_{\mathbb Q} r$ means $q < r$ in the old arithmetic.
So the book defines a type of set. A Dedekind left set. The definition makes sense. And by definition we are going to call a Dedekind left set a "real nummber". This is fine! We could have called a Dedekind left set a "pickle sandwich" if we wanted to. It does not matter that "real number" means something different in CONTWGUW. We are not ever going to use CONTWGUW ever again.
So. Is $r_* = \{q\in \mathbb Q| q\le \frac 12\}$ a 'real number' or a Dedekind left set.
No, it is not because it has a maximum element, $\frac 12$ and a 'real number' (which is a type of set) doe not have a maximum element.
Now if $q \in \mathbb Q$ and $q_* = \{p \in \mathbb Q|p < q\}$, is the set $q_*$ a 'real number'?
Your first mistake is you describe $q_*$ as "We have set q that consists of rational numbers and each its rational number has following property: namely any rational number that is less than any rational number".
It is not the set of any rational number less than any other; it is the set of all rational numbers less than $q$ which is a specific rational number.
"This is not clear what $q +{\mathbb Q} _1 \not < q$ means. Does it mean "q+1 isn't less than q when assumed that q is a rational number"?
Yes, it means exactly that.
"If yes, then why don't we just write it down as "q+1 is more than q when assumed that q is a rational number"? It's more straightforward."
Why is that more straightforward? We want to show that $q+1 \not \in q_*$ and $q+1 \in q_* \iff q+1 < q$. So we want to show it is not true that $q+1 < q$. i.e. we want to show that $q+1 \not < q$.
"Besides, if we adopt the interpretation it's unclear why should we conclude that $q_*$ is a proper subset of all rationals. "
Um, $q_* = \{p\in \mathbb Q| p< q\} \subset \{p \in \mathbb Q\} = \mathbb Q$. So it is a subset. We just need to show it is a proper subset. It is not empty because $q -1 \in \mathbb Q$. And it is not all of $\mathbb Q$ because $q + 1\not \in \mathbb Q$. So it is a proper subset.
"I'm not sure how to interpret $q-_{\mathbb Q}1 <_{\mathbb Q} q$ here and why should it mean that set $q_*$ can't be empty. My best guess is that it means "For any rational number there is always smaller rational number exists. Thus the set is NOT empty". I agree with the premise, but I don't see how the conclusion follows from it."
If means $q - 1 < q$ . Thus $q-1 \in \{p\in \mathbb Q|p < p\}=q_*$. Thus $q_*$ is not empty.
The two remaining things we have to do are:
ii) Show that if $p \in q_*$ and $r < p$ ($r$ is rational) then $r \in q_*$.
This is clear. If $p \in q_*$ then $p$ is rational and $p < q$. And if $r < p$ and $p < q$ then $r < q$ and therefore $r\in q_*$.
iii) Sow that $q_*$ has no maximum element.
If can't. If $r \in q_*$ then $r$ can not be maximal. Because $r< \frac {r+q}{2}< q$ . So $\frac {r+q}2 \in q_*$.
So All the conditions of a Dedekind left set are fullfilled.
So $q_*$ is a Dedekind left set. So it is what we are calling a 'real number'.

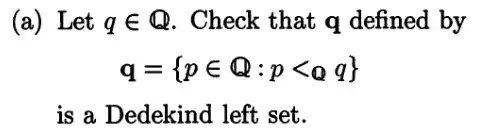
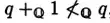 means. Does it mean "q+1 isn't less than q when assumed that q is a rational number"? If yes, then why don't we just write it down as "q+1 is more than q when assumed that q is a rational number"? It's more straightforward. Besides, if we adopt the interpretation it's unclear why should we conclude that q is a proper subset of all rationals.
means. Does it mean "q+1 isn't less than q when assumed that q is a rational number"? If yes, then why don't we just write it down as "q+1 is more than q when assumed that q is a rational number"? It's more straightforward. Besides, if we adopt the interpretation it's unclear why should we conclude that q is a proper subset of all rationals. 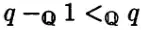 and why should it mean that set q can't be empty. My best guess is that it means "For any rational number there is always smaller rational number exists. Thus the set is NOT empty". I agree with the premise, but I don't see how the conclusion follows from it.
and why should it mean that set q can't be empty. My best guess is that it means "For any rational number there is always smaller rational number exists. Thus the set is NOT empty". I agree with the premise, but I don't see how the conclusion follows from it.