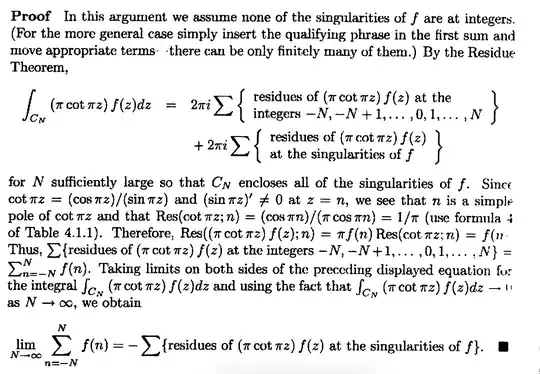2

Let $f(z)$ be a meromorphic function with a finite number of poles $a_1,\dots,a_m$, where $a_i\not\in\mathbb Z\cup\{0\}$.

Prove that if there exists a sequence of contours $\{C_n\}$ that goes to the point infinity and is such that $$\displaystyle\lim_{n\to\infty}\int_{C_n}f(z)\cot (\pi z)dz=0,$$ then $$\displaystyle\sum_{n=-\infty}^\infty f(n)=-\pi\sum_{k=1}^m\text{res} [f(z)\cot(\pi z)]_{z=a_k}$$

From Marsden book:

enter image description here

enter image description here

What does it mean the part that says

Taking limits on both sides...

If you take the limits,

$\displaystyle\lim_{N\to\infty}\sum_{n=-N}^{N} f(n)=\lim_{N\to\infty}\sum\text{res} [f(z)\pi\cot(\pi z)]_{z=n}\dots (*)$

and how do you pass from $(*)$ to $\displaystyle-\sum_{k=1}^m\text{res} [\pi f(z)\cot(\pi z)]_{z=a_k}$ ?

Could anyone explain please?

Thank you

Community
  • 1

1 Answers1

3

Taking limits on both sides of the preceding displayed equation for the integral $\oint_{C_N}(\pi\cot\pi z)f(z)dz$

This means taking the limit $N\to\infty$ on both sides of $$ \begin{align} \oint_{C_N}f(z)dz &=2\pi i\sum\text{Res $(\pi\cot\pi z)f(z)$ at $-N,\cdots,+N$} \\ &~~~~+2\pi i\sum\text{Res $(\pi\cot\pi z)f(z)$ at singularities of $f$} \\ \end{align} $$

which is $$ \begin{align} \lim_{N\to\infty}\oint_{C_N}f(z)dz &=\lim_{N\to\infty}2\pi i\sum\text{Res $(\pi\cot\pi z)f(z)$ at $-N,\cdots,+N$} \\ &~~~~+\lim_{N\to\infty}2\pi i\sum\text{Res $(\pi\cot\pi z)f(z)$ at singularities of $f$} \\ \end{align} $$

and using the fact that $\oint_{C_N}(\pi\cot\pi z)f(z)dz\to0$ as $N\to\infty$,

Therefore, $$ \begin{align} 0 &=\lim_{N\to\infty}2\pi i\sum\text{Res $(\pi\cot\pi z)f(z)$ at $-N,\cdots,+N$} \\ &~~~~+\lim_{N\to\infty}2\pi i\sum\text{Res $(\pi\cot\pi z)f(z)$ at singularities of $f$} \qquad{(*)}\\ \end{align} $$

Since for an integer $k$ $$\text{Res $(\pi\cot\pi z)f(z)$ at $k$}=f(k)$$ we can rewrite $(*)$ as $$ \begin{align} 0 &=\lim_{N\to\infty}2\pi i\sum_{k=-N}^N f(k) \\ &~~~~+\lim_{N\to\infty}2\pi i\sum\text{Res $(\pi\cot\pi z)f(z)$ at singularities of $f$} \\ \end{align} $$

Furthermore, recognizing that the second sum does not depend on $N$ for large enough $N$, we have

$$\begin{align} 0 &=\lim_{N\to\infty}2\pi i\sum_{k=-N}^N f(k) +2\pi i\sum\text{Res $(\pi\cot\pi z)f(z)$ at singularities of $f$} \\ 0 &=\lim_{N\to\infty}\sum_{k=-N}^N f(k) +\sum\text{Res $(\pi\cot\pi z)f(z)$ at singularities of $f$} \\ \end{align} $$ $$ \color{red}{ \lim_{N\to\infty}\sum_{k=-N}^N f(k) =-\sum\text{Res $(\pi\cot\pi z)f(z)$ at singularities of $f$}} $$

Szeto
  • 11,159