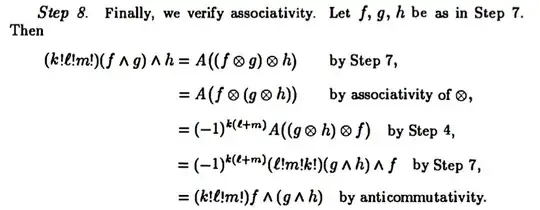Why do we need the multiple $\frac{1}{k! l!}$ in the definition of wedge product?

Question

In the book of Analysis On Manifolds by Munkres, at page 238, it is claimed that in the definition of wedge product

For alternating k-tensor $f$ and alternating l-tensor $g$ on $V$, $$f \wedge g = \frac{1}{k! l!} A (f\otimes g) = \frac{1}{k! l!} \sum_\sigma (\operatorname{sgn} \sigma) (f\otimes g)^\sigma,$$

and in order for wedge product to be associative, we need that constant multiple $\frac{1}{k! l!}$.

However, while proving the associativity of the wedge product,

I do not see and necessity for keeping that multiple in order for the product to be associative, so what am I missing in here ?

Answer 1

To answer @md2perpe's doubts, from your first equation I desume that $$A(f\otimes g) = \sum_{\sigma \in \mathfrak S_{k+l}} (\operatorname{sgn} \sigma)(f \otimes g)^\sigma, $$ or in the case of a single alternating $p$-tensor $t$, $$A(t) = \sum_{\sigma \in \mathfrak S_{p}} (\operatorname{sgn} \sigma)t^\sigma,$$ where $\mathfrak S_p$ is the group of permutations of $p$ objects. This group is itself a set of cardinality $p!$, which is part of the reason why most authors include a factor of $1/p!$ in front of the sum above. I'm surprised Munkres wouldn't define $A$ with this factorial coefficient included. If we apply the correction, i.e. if we define an alternative operator s.t. $$\operatorname{Alt}(t) = \frac 1 {p!} A(t) = \frac 1 {p!} \sum_{\sigma \in \mathfrak S_{p}} (\operatorname{sgn} \sigma)t^\sigma, $$ then the invariant space of $\operatorname{Alt}$ coincides with the space $\Lambda^p(V)$ of alternating tensors; on the other hand, the action of $A$ on $\Lambda^p(V)$ is in general a dilation/contraction. To see this, assume $t$ is alternating, i.e. $t^\sigma = (\operatorname{sgn}\sigma) t$, and compute $\operatorname{Alt}(t)$: since $(1)^2 = (-1)^2 = 1$, $$\operatorname{Alt}(t) = \frac 1 {p!} \sum_{\sigma \in \mathfrak S_{p}} (\operatorname{sgn} \sigma)t^\sigma = \frac 1 {p!} \sum_{\sigma \in \mathfrak S_{p}} (\operatorname{sgn} \sigma)^2 t = \frac 1 {p!} \sum_{\sigma \in \mathfrak S_{p}} t = \frac {p!} {p!} t = t. $$ Combining this with the fact that, for a general $p$-tensor $s \in T^p(V)$, $\operatorname{Alt}(s) \in \Lambda^p(V)$ (again just compute $(\operatorname{Alt}(s))^\sigma$ and see that it is equal to $(\operatorname{sgn} \sigma) \operatorname{Alt}(s)$), we obtain that $\operatorname{Alt}$ is a projector: $$\operatorname{Alt}^2 = \operatorname{Alt}.$$ The analogous formula with $A$ is $A^2 = p!A$ (not quite as projector-y: the coefficients accumulate over repeated application of $A$). In other words, $A$ is not the most natural alternating operator.

As for the issue with associativity, you are right that the proof you posted could be carried out without having to insert the coefficient in front of $A$. This is ultimately because Step 7 is used twice, once in the "forward" direction (transforming wedges into tensor products) and then once in the "backward" direction (rewriting tensor products as wedges). I don't know why Munkres made that claim.