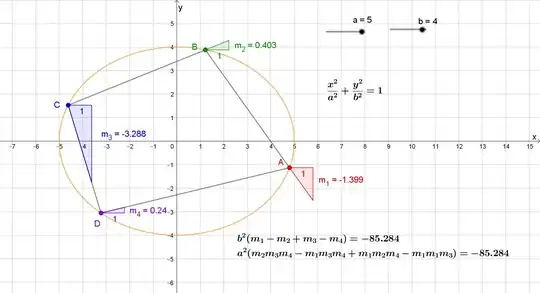
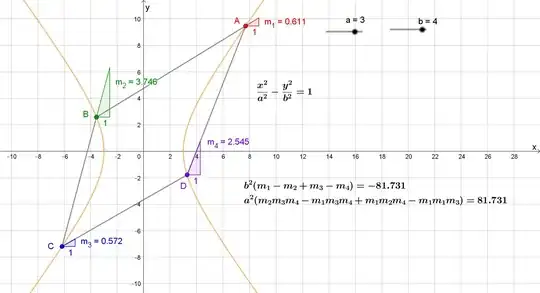
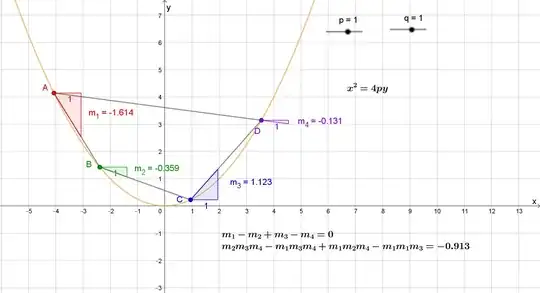
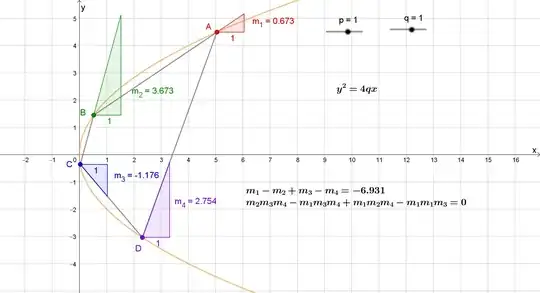
Question: Let $ABCD$ be a quadrilateral on the hyperbola $H: \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$. Let the slopes of the sides be $m_1,m_2,m_3$ and $m_4$, then does there exist a relation between $m_1,m_2,m_3$ and $m_4$ independant of the points chosen?
My Approach: Let the eccentric angles of $(A,B,C,D)$ be $(\alpha,\beta,\gamma,\delta)$. Then:- \begin{align} m_1 &= \frac{b}{a} \frac{\cos(\frac{\alpha - \beta}{2})}{\sin(\frac{\alpha + \beta}{2})} \\ m_2 &= \frac{b}{a} \frac{\cos(\frac{\beta - \gamma}{2})}{\sin(\frac{\beta + \gamma}{2})} \\ m_3 &= \frac{b}{a} \frac{\cos(\frac{\gamma - \delta}{2})}{\sin(\frac{\gamma + \delta}{2})} \\ m_4 &= \frac{b}{a} \frac{\cos(\frac{\alpha - \delta}{2})}{\sin(\frac{\alpha + \delta}{2})} \\ \end{align} How to eliminate $\alpha,\beta,\gamma,\delta$ from these equations?
[Note: The original question was to find if such a relation holds for any conic section - I was able to show it holds for a parabola and an ellipse, but for hyperbola the calculations are very difficult.]
[Note after seeing comments: For the case of a parabola and ellipse, it is possible to extend it the property for all n-gons, where n is even. I'm not sure about the hyperbola case, as I can't seem to derive the case for a quadrilateral itself.]