Minimum of repeated iteration of $n^{-x}$

Question

Consider the repeated iteration of the function $f(x) = n^{-x}$, (meaning the result from the first calculation is the argument for the next and so on)

The first value of $x$ can be any positive number, lets say 1. The number of iterations is also not too important, lets say 1000.

More important is the value of $n$, in particular: Somewhere around $14$. This repeated iteration yields its minimum value of $\approx 0.37$

Is something known about the value of $n$ which yields this minimum value, and the resulting value?

If the process converges, the limit $x$ is the root of $f(x)=x$. So you could easily derive the desired property of $n$ (if you additionally work out the question of convergence...). — metamorphy, Aug 31 '18 at 17:36
I think I've found the answer (right after posting): $n=e^e$ with the resulting value being 1\e — SmallestUncomputableNumber, Aug 31 '18 at 21:00
Possible duplicate of Is there an exact value to the minimum of the infinite tetration of $x$? — Jam, Aug 31 '18 at 22:11
Actually if you don't demand that the iteration converges, you can get lower than that with a higher $n$ and a large odd number of iterations... — hmakholm left over Monica, Sep 01 '18 at 01:08

score 1 · Accepted Answer · edited Jun 12 '20 at 10:38

Minimum of Sequence

Define $L(n)$ as the limit of the sequence $f_{i+1}=n^{-f_i}$, given $f_0=x$. We may show that $L(n)$ is strictly decreasing over $[e^{-1/e},e^e]$. But this is the only interval where $L(n)$ is convergent. Hence, the minimum of $L(n)$ is at $e^e$. However, for $n>e^e$, the sequence oscillates between two values near $0$ and $1$. In fact, the oscillating sequences have no minimum and can be made arbitrarily close to $0$, for odd $i$.

Assuming convergence, we may solve $L(n)=n^{L(n)}$ for $L(n)=\frac{W(\ln n)}{\ln n}$, where $W(x)$ is a branch of the Lambert $W$ function. And indeed, at $n=14$, we have $\frac{W(\ln 14)}{\ln 14}\approx0.37$, as you'd suggested. For the oscillating sequences, the larger we make $n$, the smaller we can make the lower limit of this sequence (i.e. the limit of the odd terms) (code).

Addenda

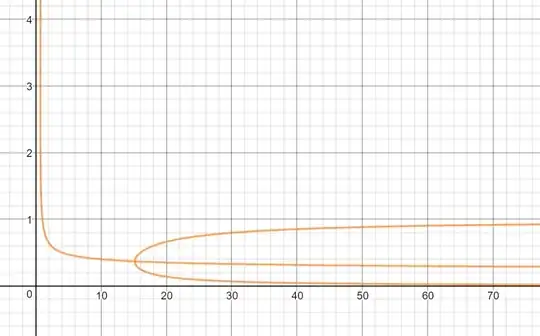
Assuming the sequence is convergent, its limit as $i\to+\infty$ is $L=\lim_{i\to+\infty}x_{i+2}=\lim_{i\to+\infty}x_{i}$ *. Hence, $L=n^{-(n^{-L})}$, which allows us to plot $L$ vs. $n$, as in the figure below (desmos). This allows us to see the fork around $n=e^e\approx15.15$ between the upper ($L\approx1$) and lower ($L\approx0$) subsequences.

I've also noticed that for the oscillating sequences ($n>e^e$), if the starting value is $x>\frac{W(\ln n)}{\ln n}$ the sequence (for odd $i$) seems to converge to the upper value $(L\approx1)$, while for $x<\frac{W(\ln n)}{\ln n}$, the sequence (for odd $i$) seems to converge to the lower value $(L\approx0)$.

* It is more useful to compare $x_{i+2}$ and $x_i$ than $x_{i+1}$, as it lets us show the oscillatory activity for $n>15$.

Regarding the effect of the starting values - we can plot $f_6$ (red) and $f_7$ (blue) as a function of $n$ and then vary the initial value $x_0$ (desmos). This shows that when $x_0$ is small, $f_6$ (and likewise for other even $i$) form the lower part of the oscillating sequences, while for odd $i$, the $f_i$ form the upper part. But conversely, when $x_0$ is large, this is reversed. — Jam, Sep 01 '18 at 14:23

Minimum of repeated iteration of $n^{-x}$

1 Answers1

Minimum of Sequence

Addenda