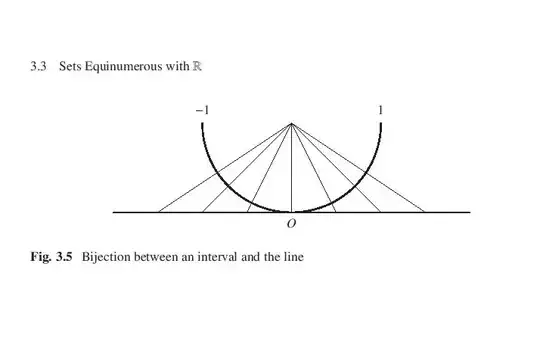
I need to prove that the interval $(a,b)$ and the set of Real numbers share the same cardinality.
I understand that I need to find a bijection between the two sets. I have been hinted to use something like $(0,1)$ or $(-1,1)$ to find a bijection then extend it to all reals. I need advice on how to set up the actual proof. Trigonometric functions are not to be used in this proof.
Any two open intervals $(a,b)$ and $(c,d)$ are equivalent via $$x \mapsto c+\Big(\frac{d-c}{b-a}\Big)(x-a)$$
Therefore $(a,b)$ and $(-1,1)$ are equivalent via $$x \mapsto -1+\frac{2}{b-a}(x-a) $$
Also $(-1,1)$ and $\Bbb{R}$ are equivalent via $$x \mapsto \frac{x}{x^2-1}$$
Finally use this fact : "Composition of bijections is again a bijection" to see $(a,b)$ is equivalent to $\Bbb{R}$
Geometrically imagine $(a, b)$ bent into a semicircle that rests on the number line at $O$, as shown in Fig. $3.5$.(replace $-1$ by $a$ and $1$ by $b$ in the figure)
Rays
from the center of the semicircle establish a one-to-one correspondence between points of $(a, b)$ and points of the line.
