How does $f(x)= x \sin(\frac{\pi}{x})$ behave?

Question

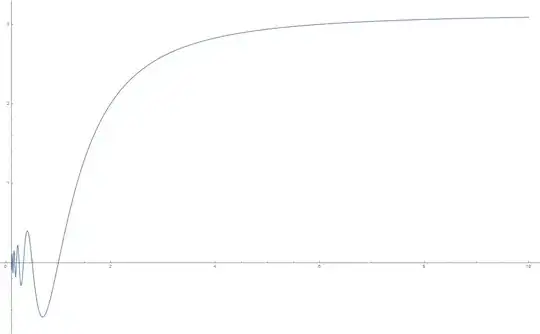
I think this function is increasing for $x>1$ but wanted to find the reason. So I thought about taking the derivative:

$f(x)= x \sin(\frac{\pi}{x})$

Aplying the chain an the product rule, we get:

$f'(x)= \sin(\frac{\pi}{x})-\frac{\pi}{x} \cos (\frac{\pi}{x})$

The function is increasing if the derative is more than or equal to $0$, so:

$\sin(\frac{\pi}{x})-\frac{\pi}{x} \cos (\frac{\pi}{x}) \ge 0$

$\sin(\frac{\pi}{x}) \ge \frac{\pi}{x} \cos (\frac{\pi}{x}) $

Since $ \cos ( x) > 0$, if $ 0< x < \pi$, $ \cos (\frac{\pi}{x}) > 0 $, because $ 0<\frac { \pi}{x}< \pi$.

$ \tan (\frac{\pi}{x}) \ge \frac{\pi}{x}$

I get to this point and don't know how to continue. I'd like you to help me or give me a hint, or maybe see a different way of showing it. Anyway, thanks.

Answer 1

You have reached the point where you want to prove that for $x>1$:

$$\sin(\frac{\pi}{x})-\frac{\pi}{x} \cos (\frac{\pi}{x}) > 0$$

If you introduce variable $y=\frac\pi{x}$, the expression becomes:

$$\sin y-y \cos y>0\tag{1}$$

It is also obvious that:

$$x\in(1,+\infty)\implies y\in(0,\pi)\tag{2}$$

Basically you want to prove (1) for values of $y$ in (2).

The full range of $y$ can be divided into two sub-ranges:

CASE 1: $y\in[\frac\pi2,\pi)$

In this particular case $\sin y>0$ and $\cos y\le0$. Obviously, the expression on the left of (1) is positive.

CASE 2: $y\in(0, \frac\pi2)$

In this particular case $\sin y>0$ and $\cos y>0$. In this case (1) is equivalent to:

$$\tan y>y$$

This is a well known fact and you can find several different explanations/proofs on the following page: Why $x<\tan{x}$ while $0<x<\frac{\pi}{2}$?

Here is the graph of $f(x)=x\sin\frac\pi{x}$:

As an exercise you can prove that $\lim_{x\to\infty}f(x)=\pi$

Answer 2

Try the Maclaurin series for tangent: $$\tan x = x + \frac{x^3}{3} + \frac{2 x^5}{15} + \ldots$$ All terms are positive when $x > 0$, so $\tan x > x$. This proves that $\tan \frac{\pi}{x} > \frac{\pi}{x}$ for $0 < x < \frac{\pi}2$.

Alternatively, define $f(x) = \tan x - x$. Then $f(0) = 0$ and $f'(x) = \sec^2 x - 1 > 0$ for $0 < x < \frac{\pi}2$, so $f(x)$ is increasing, and $f(x) > 0$ on $0 < x < \frac{\pi}2$.

Now, here's the catch: remember that tangent is not defined at $x = \frac{\pi}2$. However, the argument of your tangent function is $\frac{\pi}{x}$. So, for $x > 2$, this fraction decreases from $x = 2$ to $x = \infty$, and in fact, approaches zero. Therefore, you are safe with your argument showing that the original function is increasing for $x > 2$. For $1 < x \leq 2$, you need to be a bit more careful.